- Home
- バートランド・ラッセル, 創造認識学
- 創造認識学第一回:「ラッセルのパラドクスの論理階型理論」とはなにか(前編)
創造認識学第一回:「ラッセルのパラドクスの論理階型理論」とはなにか(前編)
- 2024/7/14
- バートランド・ラッセル, 創造認識学
- コメントを書く
Contents
はじめに
動画での説明
・この記事の「概要・要約・要旨・まとめ」はyoutubeの動画の冒頭にありますのでぜひ参照してください。
よろしければサイト維持のためにチャンネル登録をよろしくお願いしますm(_ _)mモチベになっていますm(_ _)m
バートランド・ラッセルとは、プロフィール
 (パブリックドメイン,出典)
(パブリックドメイン,出典)
バートランド・ラッセル(1872-1970)はイギリスの哲学者であり、論理学者。十九世紀末のイギリス経験論の断絶期に経験論を復興し、二十世紀初頭に集合論のパラドクスを発見して「数学の危機」をもたらし、その解決と「数学の論理学への還元」を目指した『プリンキピア・マテマティカ』を著したことで知られている。
前提の記事
※創造認識学と創造美学は創造発見学のサブカテゴリーです
根本的な内容:創造発見学第四回:「創造発見学とはなにか」
前回の内容:創造美学第一回:クリストファー・アレグザンダーにおける「生き生きとした構造」とはなにか
記事の分割について
創造認識学第一回:「ラッセルのパラドクスの論理階型理論」とはなにか(前編)
創造認識学第一回:「ラッセルのパラドクスの論理階型理論」とはなにか(中編)
創造認識学第一回:「ラッセルのパラドクスの論理階型理論」とはなにか(後編)
記事が長すぎて重いので3つに分割することにしました。動画では1つにまとめています。
ラッセルのパラドックス
基本方針
1:私はベイトソンの主張する認識論を厳密かつ体系的に理解したい。ラッセルの論理階型理論(タイプ理論)を理解するのはそのための手段である。
2:私は物理学も数学も、論理学も詳しくない。論理階型理論について専門的に説明することはできない。そのため、難解な数式や記号はほとんど扱わない。あくまでもベイトソンの主張と関連する限りの、最低限の論理階型の理解を目指す。
論理階型理論
論理階型理論とはなにか、意味、定義、わかりやすく解説
論理階型理論(タイプ理論):自己言及によるパラドックスを回避するために、この世にあるもの(存在者)をすべて階型(タイプ、オーダー)に分けて考える理論のこと。
バートランド・ラッセル(1872-1970)が提唱したといわれている。論理階型理論は「単純タイプ理論」と「分岐タイプ理論」に大きく分かれている。
悪循環原理とはなにか、意味、定義、わかりやすく解説
論理階型理論は主に以下の2つのルールを守るような論理学の体系を整備するものであり、またそのための前提を設定するものである。まずはルールだけ見ていく(この時点で理解できなくてもOK)。
- 正式な論理的・数学的言説において、「クラスはそれ自体のメンバーには決してなりえない」。
- 正式な論理的・数学的言説において、「クラスは、そのメンバーから(正しく)除外されるものの全体がつくるクラスのメンバーにはなりえない」。
このようなルール(方針、原理)をラッセルは「悪循環原理」と呼んでいる。悪循環原理を守るためにはタイプ理論(論理階型理論)が必要であるという順番。名前的にややこしいかもしれないが、悪循環を防ぐ原理という意味である。
特に参考にしたページ
・キーワード:論理階型理論における2つの主張
「まず《論理階型理論》が、どんな事柄を問題にするのか、示しておこう。この理論は次のことを主張する。――正式な論理的・数学的言説において、クラスはそれ自体のメンバーには決してなりえないこと。ものの名前は名付けられたものとは違うこと。『ジョン・ベイトソン』は、あの少年を一個のメンバーとして含むクラスであること。等々。みな、わかりきった、あえて主張するまでもないことだが、しかし、のちに見ていくように、行動科学の理論のなかに、ものの名前と名づけられたものとを混同するような――湯気たちのぼる料理をメニューの紙切れと混同するような――論理階型づけ(logical typing)のミスが見られるのは、けっして珍しくないのだ。」
『精神の生態学』,383p「この理論が主張することのなかには、それほど当たりまえではないことも含まれる。『クラスは、そのメンバーから(正しく)除外されるものの全体がつくるクラスのメンバーにはなりえない』というのがそれだ。[クラスは当のクラスの一員ではないけれども、同時に当のクラスの一員ではないものすべてから成るクラスの一員でもない。]椅子というものを一まとめにして椅子のクラスをつくるとき、個々のテーブルなりスタンドなりの傘なりは、『非・椅子』という名の巨大なクラスに属するといえる。しかし、その『非・椅子』のクラスの一項目に『椅子のクラス』は数えられない。正式な言説で、それを含めたら、誤りなのである。」
『精神の生態学』384p「では、『クラスに属さないものの全体がつくるクラス』は一個の『クラスに属さないもの』だろうか。《論理階型理論》は、これにも『否』と答える。次のように対称的に考えれば、お解りだろう。
a:非・椅子のクラスは椅子のクラスと抽象の等級(オーダー)が同じである。すなわち両者は同じ論理階型に属する。
b:椅子のクラスが椅子でないとすれば、それに相応して、非・椅子のクラスも非・椅子ではない。論理的な言説を支配するこの規則が破られるとき、パラドックスが生じ、その言説は行き倒れになる――これが論理階型理論の最後の主張点である。」
『精神の生態学』384p
悪循環原理:ある集まりが、その全体によってしか定義できない要素を含む場合、その集まりは全体を持たない。
全体を持たないということは「存在しない」、というより「存在しないということすら言えない」ということであり、ラッセルは議論の対象にすらならないという。ベイトソンの表現で言えば「なかったものとして葬ってしまう」ということである。
悪循環原理は生じてしまったパラドックスをナンセンスであり、なかったものにするというニュアンスがある。そしてタイプ理論はそもそもそうしたパラドックスを生じさせないような仕組みを整備するというニュアンスがある。対処療法ではなく、根本療法へと進んでいくというイメージだろうか。
単純タイプ理論や分岐タイプ理論という難しい話を後回しにして、先にざっくりと先程の2つのルールを具体的に理解していくことにする。
そもそも私のようにクラス(集合)とはなにか、メンバー(要素)とはなにかすら曖昧な人もいるのではないだろうか。そうした基礎的な部分を先に扱っていく。
特に参考にしたページ
・キーワード:悪循環原理の定義
「ラッセルは、パラドクスのこうした普遍的な性格に鑑みて、自分が自分自身の規定に当てはまるかどかを問うことが間違いのもとだと考えた。つまり『自己言及』を禁ずることが、パラドクスの回避の道であるとした。そこで『悪循環原理』が定式化される。悪循環原理――あつ集まりが、その全体によってしか定義できない要素を含む場合、その集まりは全体を持たない。」
三浦俊彦『ラッセルのパラドックス』,44p
クラスとメンバー(基礎知識)
クラスとメンバーとはなにか、意味、定義、わかりやすく解説
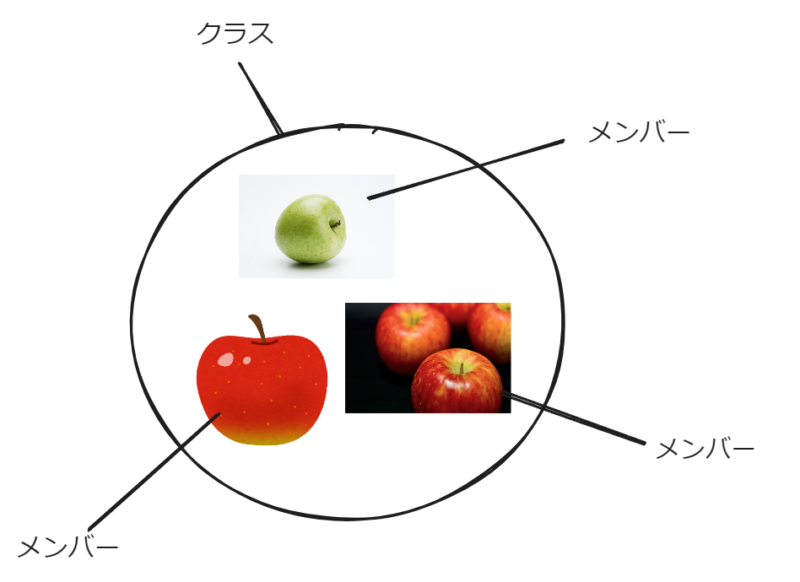
クラスとはいわゆる集合であり、要素の集まりである。たとえば私が昨日食べたリンゴ、さっき店で売られていたリンゴ、今イタリアで誰かが食べているリンゴはそれぞれ違う。「眼の前に今あるこのリンゴ」は燃えるが、「リンゴ」は燃えないという言い方をすれば区別がわかりやすいかもしれない。
それぞれの具体的なリンゴは同じリンゴというクラス(集合)のメンバー(個体、要素)である。学校のクラスは一緒だけれども、それぞれ違う生徒という言い方でも理解できるかもしれない。
図にするとこのようなイメージになる。
たとえば哺乳類というクラスには人間やゴリラがメンバーとして含まれていると考えることができる。日本人というクラスには私や近所の田中さんというメンバーが含まれていると考えることができる。
何がクラスで、なにがメンバーかは絶対的ではなく相対的?
もちろん、人間が人種の集まりとして捉えられたりする場合は人種はメンバーとなり、人間がクラスとなると考えることもできる。
また、人種を人間というクラスのサブクラスとし、さらに私というメンバーがそのサブクラスに含まれていると考えることができる。「考えることもできる」というのは私が暫定的にそう考えることにした、一般的にそう分類されているというようなものにすぎない。明日には新たな分類が合理的とされ、一般的ではなくなるかもしれない。しかし、論理学のほとんどはこうした文脈に左右されるような曖昧なものではなく、「ある前提に基づけば、ある帰結が確実に導かれる」というようなカッチリとした演繹的体系である。
論理学は「形式」を扱うものであり、人間とはなにか、人種とはなにか、それらの関係はどういうものかといった「内容」を扱うものではなく、絶対的なものではないことに注意する必要がある。そうしたものを扱うためには論理学以外の学問などを考慮する必要があるだろう。
たとえば、ラッセルは「いかなる白いものも白い」という文章すら論理的真理と認めず、「ある性質について、その性質をもついかなるものも、その性質をもつ」と言えばようやく論理的真理と認められるという。また、「いかなるクラスでもない最小の構成要素とはなにか」というテーマもラッセルでは重要になるので面白い(ベイトソンでも)。
ラッセルのパラドクス
パラドクスとはなにか、意味、定義、わかりやすく解説
パラドクス:一般に、「正しい前提から正しい推論を経て間違った結論(たとえば矛盾)に至る」現象を指す。
個人的にパラドクス(パラドックス)という言葉はややこしい。なぜなら、パラドクスだからといって必ずしも矛盾していないというニュアンスがあるからだ。たとえば循環論法や論点先取りは必ずしも矛盾とはいえないが、しかし間違った結論を引き起こすことがあり、パラドクスとも表現できる。このことを念頭においておく。
特に参考にしたページ
・キーワード:パラドクスの定義
「総じてパラドクスとは、『正しい前提から正しい推論を経て間違った結論(たとえば矛盾)に至る』現象を指す。論理上は、『正しい前提』に『正しい推論』を適用すれば必ず『正しい結論』が出てくるのに。どこがおかしかったのか。解決としては、前提が間違っていたか、推論が間違っていたか、結論が実は間違っていないのか、のどれかとなるだろう。」
三浦俊彦『ラッセルのパラドックス』,9-10p
ラッセルのパラドクスとはなにか、意味、定義、わかりやすく解説
ラッセルのパラドックス:「自分自身を含まない集合の集合」を考えたとき、それが自分自身を含むかどうかでパラドクスが生じる問題のこと。
より詳しくいうと、「自分自身の要素ではない集合の集合」(集合R)というものを考えた場合、この集合Rが「自分自身の要素ではない」と仮定しても、「自分自身の要素である」と仮定してもパラドクスが生じてしまうような事態のこと。
この定義だけを単体で見ると、論理学に疎い人は何を言っているか、よくわからない。具体的にゆっくり後で見ていくことになる。
ラッセルのパラドクスは床屋のパラドクス、嘘つきのパラドクス、グレリングのパラドクス、ベリーのパラドクスなどの日常言語に置き換えられて説明されることがある。
床屋のパラドクスは「論理的パラドクス」であり、それ以外のパラドクスは「意味論的パラドクス」と分類されることがある。たとえば嘘とはどういう状態なのか、名付けるとはどういう状態なのかというのは論理学の範疇ではない、とラッセルは批判されることがある。純粋に論理的で形式的なものが論理的パラドクスと考えるイメージなのだろう。いずれも純粋なラッセルのパラドクスと類似しているが、論理的な言語を日常言語によって具体化したという点で曖昧さを含み、厳密には同じではないのかもしれない。
今回は「床屋のパラドクス」と「ベリーのパラドクス」を主に扱う(ベリーのパラドクスは後半に)。
まずは論理的パラドクスを日常言語をできるだけ使わず、かつ難しい論理学の記号や数式も使わずに形式的な形で見ていくことになる。ここで完全に理解する必要はなく、後でさらに具体例を見ていく。
特に参考にしたページ
・キーワード:ラッセルのパラドクスの説明
「ラッセルのパラドクスは周知だと思われるが,「自らを要素としない集合をすべて集めてできた集合は,自らを要素とするであろうか」というものである。たいていの集合が「自らを要素としない集合」である。たとえば,「犬」という集合の要素は,柴犬だったりブルドッグだったり,あるいは飼い犬のポチというように,何か具体的な個体である。決して「犬」のイデアなるものは含まれない。こうした集合全体を考えた場合,要素と「する」と仮定すると「しない」という定義に反し,「しない」と仮定すると「する」を要請されるわけである。これは,「すべての集合の集合」という,無限を囲い込む思考実験に必然的に伴う問題である。では他方,「自らを要素とする集合」とは何であろうか。たとえば,「言葉」という集合はどうであろう。「言葉」というのも言葉である。また,「私の思考」という集合は。「私の思考」も私の思考の一部である。こうした集合の場合,パラドクスは起こらない。」
鈴木啓司「新たなる認識論理の構築14 集合論を超えて 境界についての認識論的考察」,48p
純粋なラッセルのパラドクスの例(論理的パラドクス)
まず、「自分自身の要素ではない集合」とはなにか。
たとえば「自分が飼っている犬」や「近所の犬」をメンバーとしてもつような「犬という集合」を考える。この場合、「犬という集合」の中にメンバー(要素)として「犬という集合」は入らないだろう。それゆえに、「犬という集合」は自分自身の要素ではない、つまり自分自身を要素として含まない集合である。他にも人間、食べ物、コンピューターなど、我々が挙げるような集合はほとんど「自分自身の要素ではない集合」である。
従って、「自分自身の要素ではない集合」の「集合」ということは、我々が考えるようなほとんどの集合をメンバーとするような集合となる。犬という集合や人間という集合など、さまざまな集合がメンバーとして入ることになる。
このような大きな集合を集合Rと表現しておく。
(1)集合Rが「自分自身の要素ではない」と仮定する
つまり、集合Rという集合の中に、集合Rというメンバーはないと仮定するわけである。これは犬というクラスの中に犬というクラスがメンバーとして入ってこないという仮定と似ている。
しかし、もし集合Rが「自分自身の要素ではない」ならば、集合Rは「自分自身の要素ではない集合の集合」であるので、集合Rの要素になっていなければならなくなる。つまり、集合Rは「自分自身の要素ではない」と仮定したのにも関わらず、「自分自身の要素である」というパラドクスが生じる。
(2)集合Rが「自分自身の要素である」と仮定する
もし集合Rが「自分自身の要素である」ならば、集合Rは「自分自身の要素ではない集合の集合」であるので、「自分自身の要素ではない集合」でなければならない。つまり、「自分自身の要素である」と仮定したのにもかかわらず、「自分自身の要素ではない」というパラドクスが生じる。
結論:「自分自身の要素ではない集合の集合」(集合R)というものを考えた場合、この集合Rが「自分自身の要素ではない」と仮定しても、「自分自身の要素である」と仮定してもパラドクスが生じてしまう。これがラッセルのパラドクスである。
特に参考にしたページ
・キーワード:ラッセルのパラドクスの説明
三浦俊彦『ラッセルのパラドックス』,39-41p
床屋のパラドクス
床屋のパラドクスとはなにか、意味、定義、わかりやすく解説
床屋のパラドクス:ある村に一軒しかない床屋は、自分で髭を剃らない村人全員の髭だけを剃る。さて、村人の一人であるこの床屋自身は、自分の髭を剃るのか、剃らないのか。
床屋のパラドクスはラッセルのパラドクスを日常言語によって具体化したものとして知られているらしい。
(1)床屋が自分で自分の髭を剃ると仮定する
床屋は自分で自分の髭を剃ると仮定してしまうと、自分の髭を剃ってはならないことになる。
なぜなら、「自分で髭を剃らない村人全員の髭だけを剃る」からである。村人の中に自分が含まれているので、自分で髭を剃ることはできない。
(2)床屋が自分で自分の髭を剃らないと仮定する
床屋が自分で自分の髭を剃らないと仮定してしまうと、自分の髭を剃らなければならないことになる。
なぜなら、「自分で髭を剃らない村人全員の髭だけを剃る」からである。村人の中に自分が含まれているので、自分で髭を剃らなければならない。
このように、どちらに仮定しても反対の結果が生じてしまい、「剃る、かつ剃らない」のようなパラドクスが生じてしまっているケースである。
ここで重要なのは「村人全員」という集合の中に、自分が要素として含まれているということである(自己言及的)。
この矛盾は、ラッセルのパラドクスにおける「自分自身を要素とするかどうか」の矛盾と類似した構造を持っていると考えることができる。
(1)ラッセルのパラドクスでは、自分自身を要素としない集合全体の集合が存在するかどうかを考えることで矛盾が生じる。
(2)床屋のパラドクスでは、自分で髭を剃らない村人全員の髭を剃る床屋が自分の髭を剃るかどうかを考えることで矛盾が生じる。
特に参考にしたページ
・キーワード:床屋のパラドクスの説明
三浦俊彦『ラッセルのパラドックス』,42-43p
ルール1、「自分自身を含む要素全体の集合」を集合と認めない
R = { | ∈ }
「自分自身を含む要素全体の集合」を記号化すると、以下のようになるらしい。
R = { | ∈ }
(1)Rは「集合」を意味する。(2){要素の表現 ∣ 条件} ※集合の要素を選ぶための条件。(3)∈は「属する」と読む。
自分自身(x)を含む集合(x)という条件を満たす、集合(x)ということになる。こうした集合Rを集合と認めない、というルールが必要だとラッセルはいう。
端的に言えば、「クラスはそれ自体のメンバーには決してなりえない」というルールが必要になる。
ラッセルはそうしたルールを破るとパラドクスが生じると考えたからだ。
たとえばリンゴというクラスには赤リンゴや青りんごといったメンバーがあることは理解できる。しかしリンゴというクラスにリンゴというクラスというメンバーが含まれてくると、「どこかおかしい」となるのではないだろうか。論理学に疎い私でも直観的にそう感じる。教室の中にAさん、Bさん、Cさん・・というメンバーと同列的に「教室さん」が座っているような違和感である。
特に参考にしたページ
キーワード:数式の参考に
離散数学 | 植野真臣研究室 – 電気通信大学
論点先取り、循環論法に陥ることもパラドクス?
たとえば哺乳類というクラスは、主に帰納的に決められていく。複数の動物に「母乳で子供を育てるという行動」が見られたとする。つまり、メンバーの共通点を一般化して見出したわけである。
ここで重要なのは、メンバー単体では哺乳類というクラスは導き出されないという点である。人間やゴリラ、クジラなどはそれぞれ「違う」けれども、「同じ」要素をもっているというような比較によって生まれるのである。
一方で、メンバーが一体しかいない「類」を考えることは理論的に可能では、と私は疑問が生じる。しかし帰納によって分類するという例では、あまり現実的ではないケースではないだろうか。帰納的一般化にはなんらかの「差異」が必要になり、「差異」は異なる個体があってはじめて成り立つからである。「いままでの分類に属していない」、「一体しかメンバーに含まれない」というのは結局「比較」が必要であり、一体のメンバー単独で見出されるものではない。
帰納におけるメンバーの比較において、そのメンバーに「哺乳類」が並んでいたらおかしい。つまり、自分を使って自分を生み出そうとしている形になる。メンバーの比較によってクラスが生じるのにも関わらず、すでにメンバーにクラスがいるのである。
こうした状態を「自己言及的」と表現する。論理学の世界では「循環論法」や「論点先取り」といわれ、論理的誤謬の一種と扱われる。ラッセル的にいえばタイプミスであり、論理階型の混同である。
正直な話、式単体で私には「矛盾」が生じているとは思えない。Aかつ非Aのような状態が生じているとは思えない。
なんとなく、循環論法的だなとか、赤いリンゴというメンバーとリンゴというクラスをごちゃごちゃにしちゃよくないよね程度の論理的ミスなら理解できる。
しかしパラドクスの定義は必ずしも「矛盾」を意味せず、「誤り」が含まれていると考えていくことができる。そしてラッセルの時代以前の集合論においては、正しい前提と正しい推論であると思われており、それにも関わらず誤りが生じてしまっていたという点が重要になる。こうした事態を「パラドクス」と表現することは理解できる。
そしてラッセルは正しい前提が実は正しくないのではないか、と思い修正を試みるようになる。具体的には「無制限変項の原理」が修正されていくことになる。無制限変項の原理をタイプ(階型)ごとに適用する、というタイプ理論によって修正していくわけである。要するに、無制限変項の原理の範囲をより限定的にしたというわけである。
ルール2、「自分自身を要素として含まない要素全体の集合」を集合と認めない
R = { | ∉ }
「自分自身を要素として含まない要素全体の集合」を記号化すると、以下のようになるらしい。
R = { | ∉ } ※∉は属さないという意味
ラッセルは集合を以下の2つに分け、またすべての集合は以下の2つのどちらかだと仮定した。
第一のグループ:自分自身を要素として含まない集合。例:人間の集合、椅子の集合など。R = { | ∉ }/p>
第二のグループ:自分自身を要素として含む集合。例:集合の集合、抽象物の集合など。R = { | ∈ }
先ほど、自分自身を要素として含む集合を集合として認めないということを学んだ。つまり、第2グループの否定である。
有名な第二グループに「集合の集合」がある。あらゆる集合を「集合の集合」というクラスはメンバーとしてもっている。しかし「集合の集合」というクラスも「集合」であり、メンバーである。
したがって集合の集合というクラスは集合の集合というメンバーをもつ必要がある。これは自己言及的である。
抽象物の集合も、「抽象物の集合」が抽象物なので、同様のケースである。
自己言及的な集合は自分の靴紐をひっぱって自分を宙にもちあげるような、ナンセンスなイメージと表現されることがある。
特に参考にしたページ
・キーワード:第一のグループ、第二のグループ
「集合を2つに分けよう。第一のグループは、自分自身の要素ではない集合。第二のグループは、自分自身の要素である集合。定義上、この2つのグループですべての集合は尽くされている。」
三浦俊彦『ラッセルのパラドックス』,37p
R = { | ∉ }はそれ単体ではおかしくない?
その点、第一グループであるR = { | ∉ }集合として認めていいのではないか、と思ってしまう。
たとえば「人間の集合」という場合に、私やあなたはメンバーとして含まれるが、「人間の集合」はメンバーとして含まないという話だ。私たちが思いつくような集合はほとんどこの第一グループに属しているという。たしかに集合の集合のようなものは例外だろう。人間の集合、マウスの集合、机の集合、服の集合など、いくらでも挙げられる。どうしてわざわざこの集合を否定する必要があるのか。※実は自己言及的なものが現実世界ではたくさんある、という話は次回のベイトソンで扱う。
ここからが面白い。ラッセルによると、ルール1をまもったとしても、問題が生じるケースがあるというのである。
この問題は私にも「矛盾」が生じていると理解できる例である。
追記(2024/07/12):R = { | ∉ }単体では不都合がないが、全てのR = { | ∉ }からなる集合R2のような集合を考えると不都合が生じてしまう。これは、Rのような集合を集合として認めてしまっているからだ。それゆえに、Rを集合として認める事はできない。そういう話だろう。たとえばゲームでは組み合わせによっておそろしく強い効果を発揮するようなものがある。単体ではあまり強くないのにも書か関わらず、2つの効果が合わさって、ゲーム自体をバグらせてしまうような(あるいは一瞬で勝利してしまうような強すぎる)ものを考えてみる。それゆえに、どちらか、あるいは両方を「禁止」するのである。たとえばカードゲームではそれが「禁止カード」と言われ、存在自体が否定される。
ルール1だけを守ったとしても、矛盾が生じてしまうケース
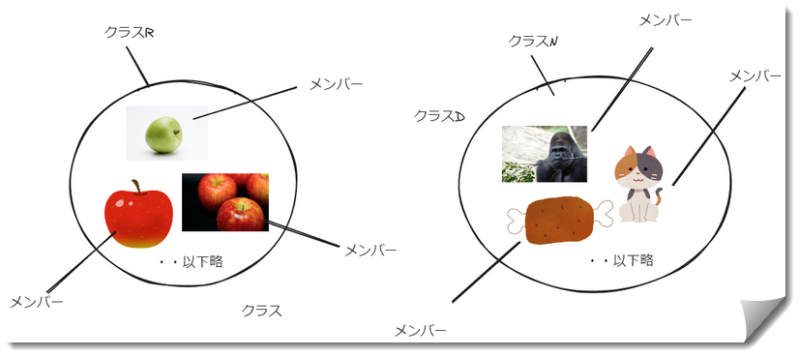
例えば、この緑のリンゴ、あの赤いリンゴといったあらゆるリンゴのメンバーの集合であるリンゴというクラスを考えてみる。このクラスをRとする。
次に、あらゆるリンゴのメンバーを含まないクラスを考えてみる。このクラスをNとする。このクラスNには肉や魚、猫やゴリラなど、リンゴというクラスのメンバー以外のあらゆるメンバーが含まれている。
さて、ここで集合R(クラスR)はクラスNの要素か、それとも要素ではないか。
つまり「あらゆるリンゴの集合」は「あらゆるリンゴのメンバー以外のメンバーを全て含む集合」に属するのかどうかという話である。
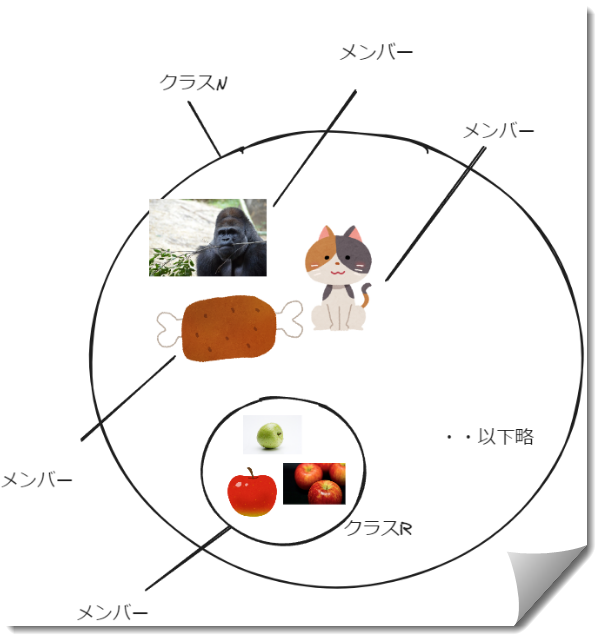
(R= {| ∈ }を集合として認めないというルール1より、リンゴというクラスはリンゴというクラスのメンバーではない。したがって、リンゴというクラスはクラスNのメンバーとなる。
つまり、リンゴというクラスRは、R = { | ∉ }ということになる。ルール2ではR = { | ∉ }を集合として認めないというものであった。認めるとどんなことが生じるかを見ていくことになる。
ここで問題が生じる。クラスNはあらゆるリンゴのメンバーを含まないクラスであったはずである。しかしクラスRを含むということは、そのメンバーを間接的に含むということにもなってしまうのではないか。
つまり、「クラスNはあらゆるリンゴのクラスのメンバーを含まない」といっているにもかかわらず、「間接的にリンゴのクラスのメンバーを含んでいる」ことになってしまう。こうした自己準拠に起因するようなパラドクスをラッセルのパラドクスという。
(1) R = { | ∈ }を認めるとパラドクスが生じる。だからこうした集合を認めない。
(2) R = { | ∉ }を認めてもパラドクスが生じる。だからこうした集合も認めない。
(3)この2つに共通しているのは、自分を定義するのに自分を含めるとか、含めないとかいう自分への言及(自己言及)が必要になるからである。2つの集合を集合として認めないような体系の整備が必要となる。ラッセルはタイプ理論などで対応しようとした。現代集合論ではツェルメロ=フレンケル集合論などがその例らしい。
【疑問】直接的に含む、間接的に含む?
・一端、私の中で生じた疑問を整理する。
論理学に疎い私には「リンゴというクラスがクラスNのメンバーになるという事態」がいまいち理解できない。これ単体でみると、リンゴというクラスの中のメンバーを「直接的」にはメンバーとして持っていない。たとえばある人Xが「人間が好き」と言っているからといって、「Xが田中さんを好き」だとは限らない、といえば何となく納得してしまう。しかし「間接的」にはメンバーとしてもつことになるという考えもできる。「人類」の中に「田中さん」も要素として含まれているからである。
他の比喩も使ってみよう。バラバラのクッキーが入った袋が入ったビニール袋というものがあるとする。たしかにビニール袋に直接バラバラのクッキーが入っているわけではないが、ビニール袋の中に入っているだろう。つまり、間接的には入っている。
そもそも「人間が好き」などという言葉が曖昧なのだろう。我々は人間というクラスに含まれる全てのメンバーが好きだという意味で「人間が好き」を使っているのだろうか。「全てのメンバーのうち、ほとんどが好き」だとか、「一部が好き」だとかそういう意味で使っているかもしれない。どういう意味で使っているかなど、よく考えずに使っている。
こうした曖昧なもの(非可述的なもの)を明瞭なもの(可述的なもの)へと還元するとどうなるか。私には正直わからない。「優しい人が好きだ」という意味で実は使われているかもしれない。しかし「優しい人」という言葉も曖昧である。もしかしたら今まで会ってきた特定のAさん、Bさん、Cさんが好きだという意味で使われているかもしれない。ここまで還元すると、AでもBでもCでもない田中さんが好きとは限らない、ということに納得できる。
もっと抽象度を上げて考えてみる。たとえばA,B,Cと言う要素をもつRというクラスがあるとする。
そして、A,B,Cという要素以外の全ての要素を持つNというクラスがあるとする。この場合、NというクラスはRというクラスをもつことになる。なぜなら、ルール1より、R = { | ∈ }を集合と認めないからである。それゆえにR = { | ∉ }となる。従って、NはRというクラスをもつ。
この場合、Nというクラスは直接的にA,B,Cという要素を持つことになるわけではない。
しかし、Nというクラスは間接的にA,B,Cという要素を持つことになる。なぜなら、NというクラスはRというクラスをもち、RというクラスはA,B,Cという要素を持つからである。
それゆえに、A,B,C以外の全ての要素を持つNというクラスが間接的とはいえA,B,Cという要素を持つことになる。それゆえに、矛盾が生じる。
もし仮に、「直接的にA,B,C以外の全ての要素を持つ」とNクラスが定義されていれば話は別だが、しかしそうではない。結局は直接的にせよ間接的にせよ、矛盾が生じることになる。
これ以上話をややこしくすることは避けたいが、しかし疑問がある。「食べ物」というクラスはクラスRのメンバーではないので、当然クラスNのメンバーとなるだろう。しかし「食べ物」というクラスはリンゴというクラスをメンバーとしてもっている。これで先程の問題と同じような矛盾が生じる。
あるいは、食べ物というクラスはいちいちサブクラスを通す必要がない、と考えることもできる。例えばリンゴというクラスや果物というクラスを通して間接的に「あのリンゴ」をもつのではなく、食べ物が「あのリンゴ」や「そのカレー」といった個物を持つと表現すればいい。とはいえ、Nクラスは食べ物というクラスをもつかぎり、やはり間接的にクラスRのメンバーをもつことになってしまうので矛盾が生じる。そのため、ルール1やルール2が必要である、という結論になるのだろう。
参考文献リスト
今回の主な文献
三浦俊彦「ラッセルのパラドクス: 世界を読み換える哲学 (岩波新書 新赤版 975)」
三浦俊彦「ラッセルのパラドクス: 世界を読み換える哲学 (岩波新書 新赤版 975)」
汎用文献
米盛裕二「アブダクション―仮説と発見の論理」
トーマス・クーン「科学革命の構造」
真木悠介「時間の比較社会学」
モリス・バーマン「デカルトからベイトソンへ ――世界の再魔術化」
モリス・バーマン「デカルトからベイトソンへ ――世界の再魔術化」
グレゴリー・ベイトソン「精神と自然: 生きた世界の認識論」
グレゴリー・ベイトソン「精神の生態学へ (上) (岩波文庫 青N604-2)」
グレゴリー・ベイトソン「精神の生態学へ (上) (岩波文庫 青N604-2)」
マックス・ウェーバー「社会科学と社会政策にかかわる認識の「客観性」」
マックス・ウェーバー「社会科学と社会政策にかかわる認識の「客観性」」
参考論文
・離散数学 | 植野真臣研究室 – 電気通信大学(URL)
・土屋盛茂「パラドックスとラッセルのタイプ理論」(URL)
・鈴木啓司「新たなる認識論理の構築14 : 集合論を超えて 境界についての認識論的考察」(URL)
・久木田水生「ラッセルの記述の理論とタイプ理論の関係について」(URL)
・池田真治、伊藤遼、久木田水生「タイプ理論の起源と発展」(URL)
コメント
この記事へのトラックバックはありません。








この記事へのコメントはありません。