創造法編集社

はじめに

動画での説明

・この記事の「概要・要約・要旨・まとめ」はyoutubeの動画の冒頭にありますのでぜひ参照してください｡

よろしければサイト維持のためにチャンネル登録をよろしくお願いしますm(_ _)mモチベになっていますm(_ _)m

バートランド・ラッセルとは、プロフィール

(パブリックドメイン,出典)

バートランド・ラッセル(1872-1970)はイギリスの哲学者であり､論理学者｡十九世紀末のイギリス経験論の断絶期に経験論を復興し､二十世紀初頭に集合論のパラドクスを発見して「数学の危機」をもたらし､その解決と「数学の論理学への還元」を目指した『プリンキピア・マテマティカ』を著したことで知られている｡

前提の記事

※創造認識学と創造美学は創造発見学のサブカテゴリーです

根本的な内容:創造発見学第四回:「創造発見学とはなにか」

前回の内容:創造美学第一回:クリストファー・アレグザンダーにおける「生き生きとした構造」とはなにか

記事の分割について

創造認識学第一回:「ラッセルのパラドクスの論理階型理論」とはなにか(前編)

創造認識学第一回:「ラッセルのパラドクスの論理階型理論」とはなにか(中編)

創造認識学第一回:「ラッセルのパラドクスの論理階型理論」とはなにか(後編)

記事が長すぎて重いので３つに分割することにしました｡動画では１つにまとめています｡

還元公理

還元公理

還元公理とはなにか､意味､定義､わかりやすく解説

任意の命題関数がその変数に関してある特定の形で表現できることを主張している｡

還元公理はタイプ・オーダーの二次元的な分岐を､一元的なタイプの階層へと整理する公理だという｡

あるいは「クラスに関してオーダーの区別を消去してくれること」とも表現されることがある｡

・特に参考にしたページ
キーワード:還元公理､整理
三浦俊彦『ラッセルのパラドックス』,81p

「還元公理――いかなる属性についても､それと同値な(=全く同じ項たちにあてはまる)述語的属性がある｡」
池田真治、伊藤遼、久木田水生「タイプ理論の起源と発展」,81p

「還元公理は､タイプ・オーダーの二次元的な分岐を､一元的なタイプの階層へと整理する公理だ｡これは､便宜的な装置のようにも見えるが､哲学的にかなり興味深い含みを持つ｡『偉大な将軍に必要な述語的属性をすべて持っていた』という属性Fは､第２オーダーの非述語的属性だが､この属性Fは､何らかの第一オーダーの､つまり述語的な属性と実は同じものだというのだ｡」
池田真治、伊藤遼、久木田水生「タイプ理論の起源と発展」,81p

オーダーの区別を消去してくれる？

どうして還元公理がオーダーの区別を消去するのか｡消去してしまったらパラドクスがまた生じてしまうのではないか､と思ってしまう｡しかし厳密にはオーダーを消去するというより､実質的にオーダーはないのも同然だ､というイメージになるのかもしれない｡

なぜなら､異なるオーダーのそれぞれの属性が実質的に同じ属性だとみなすからである｡分けるのをやめるのではなく､分けられたものを同じだと見なすのである｡例えば「偉大な将軍に必要な述語的属性を全てもっている」という属性はn+1オーダーであり､具体的な「勇敢」などの属性はnオーダーである｡しかし､n+１オーダーはnオーダーに還元できる､一致できるという考え方を導入するのである｡たとえばaかつbかつc…というように無限に列言していく形で等価(同値)とみなすわけである｡

例としては適切かどうかはわからないが､すこし考えてみよう｡例えばオレンジジュースを凍らせるとする｡再び解凍すると､オレンジジュースが得られる｡この場合､凍ったオレンジジュースと解凍されたオレンジジュースは､同じ物体の異なる表現といえるのではないだろうか｡

厳密にはすこし違うだろうとかいう考え方は隅に置くとこの考え方はわかりやすいと考える｡高いオーダーの属性も､低いオーダーの属性に還元できる｡還元できるというのは言い換えれば同じであり､「互いに同値な属性」と表現される｡

将軍の例で考えてみる

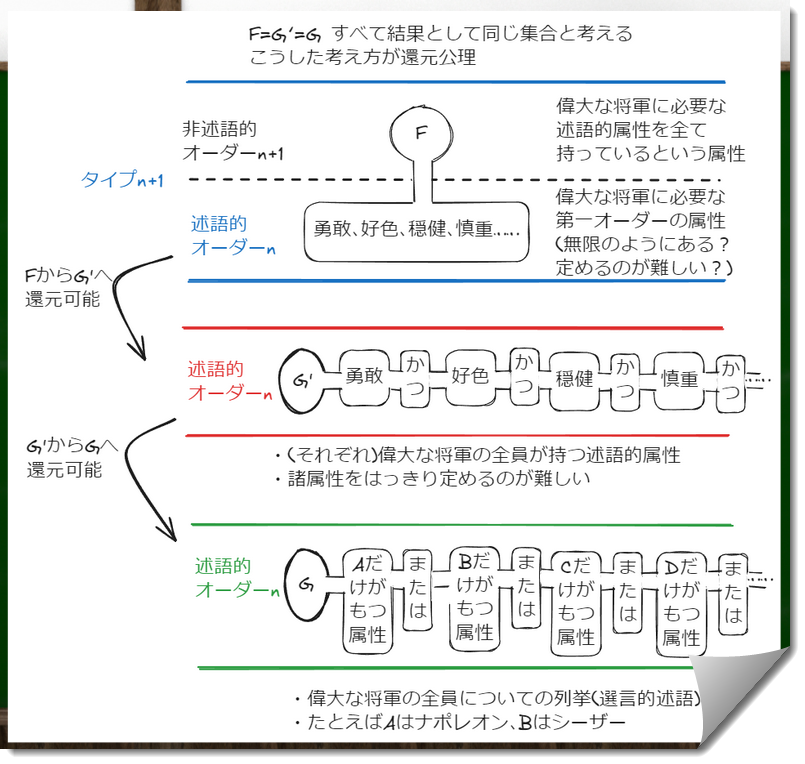
(１)「偉大な将軍に必要な述語的属性を全て持っているという属性」=Fはn+1オーダーである｡

(２)具体的に勇敢､好色､穏健…と属性を無限のように挙げていって得られる集合(F以外)はnオーダーである｡

(３)nオーダーにある具体的な属性をすべて「かつ」で結びつけていく｡

全ての属性をもっている必要があるので､勇敢であり､かつ好色であり､かつ穏健であり・・・と無限のようにある属性を列挙してつなげていく(F以外)｡このようなオーダーをG’と表現する｡

(４)さらに具体的な偉大な将軍が特有にもつ属性を列挙していくオーダーを考える｡そうしてA(例えばナポレオン)だけがもつ属性､またはBだけがもつ属性といったように列挙していき､それらを「または」で結びつけていくそうだ｡

こうしてまとまった長い述語を「選言的述語」というらしい｡述語が複数の選択肢のうちいずれかであることを示すということだ｡こうした長い述語をGと表現する｡

三浦さんの図(『ラッセルのパラドックス』,82p)を参考に作成した｡

還元公理によって､F=G’=Gとなるという図である｡FはG’に還元することができ､G’はGに還元することができる｡

ここで重要なのは「どんな非述語的属性も､他の述語的属性に還元することができる」という点である｡

こうして考えると､何かを具体的に分かりやすく説明したり､比喩を使って説明したり､まるで違った表現で説明する行為とすこし似ていると感じた｡つまり､同値の属性に適切に還元できるということが､説明の能力に関連してそうであり､深い理解の証となりそうである｡ベイトソン的にいえば(トートロジーであるにも関わらず)「理解のボーナス」が多角的な説明によって生じるという点が重要になる｡

・特に参考にしたページ
キーワード:選言的述語
「これは､言われてみればその通りだろう｡偉大な将軍の一人一人について､彼だけが持っていて他の何物も持っていない述語的属性を選び出そう｡ある瞬間に特定の言葉を発した､という属性でもいいし､出生時の正確な場所と時刻でもいい｡各々の偉大な将軍についてそうした述語的属性を少なくとも一つ選んで列挙し､それを『または』で結んだ長い述語を作ろう(『選言的述語』と呼ばれる)｡この述語Gは､いささか人工的だとはいえ､第一オーダーの述語的属性であることに変わりはない｡『すべての属性』に言及した属性ではないからである｡こうして､非述語的属性F『偉大な将軍に必要な述語的属性をすべて持っていた』は､述語的属性Gに還元できる｡他のどんな非述語的属性についても､似たような還元の工夫ができるだろう｡反例を発見した人はいない｡還元公理は正しそうだ｡」
三浦俊彦『ラッセルのパラドックス』,83p

還元公理を導入する理由

ラムジー､ウィトゲンシュタイン､ゲーデル､クワインからラッセルへの批判

還元公理がない場合の分岐タイプ理論でどういう問題が生じていたか､という点を理解するといいのかもしれない｡

たとえば「非可述的定義を含む実数論､したがって解析を十分に展開できない」という問題があったそうだ｡何を言っているか私には理解出来ない｡

しかし三浦さんの「数学の根本に矛盾があるというのは致命的な病気なので､それを治すことは何よりも優先されなければならないが､悪循環原理は､あまりに多くのものを禁じすぎて､矛盾追放後のクオリティ・オブ・ライフを保証できていないというべきだろう」という表現ですこし理解することができた｡

単純なタイプ理論ですら多くのものを禁じており､分岐タイプ理論でさらに多くのものを禁じてしまったというイメージだろうか｡

では還元公理の導入で「非可述的定義を含む実数論」が可能になったのか､という話は私には理解できない｡おそらく可能になったのだろう｡

しかし問題は還元公理が正しいかどうかである｡これに対してたくさんラッセルは批判されたらしい｡ざっくりいえば還元公理の導入を正当化する論証を欠いているそうだ｡もともとラッセルがタイプ理論を構築した理由は悪循環原理の徹底であり､その特殊論のうちに論理的パラドクスの解消や意味論的パラドクスの解消というものがあった｡しかし徹底させればさせるほど数学の大部分が困難になってしまうという問題があった｡

ラムジーによって意味論的パラドクスをそもそも論理学や数学で解消する必要があるのか､などという批判も出ている｡ラムジーは還元公理が帰納的なものである(演繹体系ではない)という批判も行っている｡さらにラムジーは「無限連言」という代わりの方法も提案したそうだ｡

他にもウィトゲンシュタインが「還元公理が考えられない世界も考えられる」と批判したらしい｡

たとえばゲーデルは悪循環原理の要求が高すぎる点､無限連言による方法は無限の直観が入りこまざるを得ない点などを批判している｡

また､ゲーデルはラッセルのオーダーの定義にはテクニカルな問題があると考えたそうだ｡ゲーデルは「外延の同一性を担保に非可述的命題関数を容認し､悪循環原理を事実上放棄した」という｡なかなか難しく何を言っているか分からないが､おそらく還元公理の良さは認めつつも､オーダーという考え方に問題があると考えたのだろう(？)｡

ラッセルの目的は数学を論理学によって展開することであり､悪循環原理の徹底によって要請されるタイプ理論によって数学の大部分が困難になるというのは問題だということはわかる｡

その困難さを解決するために都合よく､その場しのぎで(アドホックというらしい)還元公理を導入するのはよくない､と批判を受けたというわけだ｡

「そもそも非述語的属性が述語的属性に還元されるということがわかっているなら､始めからオーダーなどで分けなければいい」というクワインの批判もあったそうだ｡

三浦さんの説明では「タイプはリアルな違いだが､オーダーは語り方､表現法の違いに過ぎない」というわけである｡

・特に参考にしたページ
キーワード:クワイン､語り方
「どうせ述語的属性だけで話が済むというならば､始めからオーダーなど分けなければいのに､と思われるだろうか｡実際､そのような批判をクワインが述べている｡タイプの違いは論理的にリアルな違いだが､オーダーの違いはリアルな違いではなく､単に語り方､表現の方の違いにすぎないのだから､尊重する必要があろうか｡」
三浦俊彦『ラッセルのパラドックス』,83p

「ところが、分岐タイプ理論を含む『プリンキピア』の体系は、その複雑さや非生産的側面に関して他の陣営から厳しく批判された。分岐タイプ理論の目的は、悪循環を含みうる非可述的定義の全面禁止によって確実な基礎を築くことだった。だがそのままでは、非可述的定義を含む実数論したがって解析を十分に展開できない。そこで、ラッセルらは、分岐タイプ理論を十全に展開するために、非可述的定義を部分的に可能にする「還元公理」を要請する。それは、任意の命題関数に対し、それと外延を等しくする可述的関数が存在するという公理である。しかし還元公理は、直観を欠いたアドホックな前提にすぎず、その必要もないと散々に批判された。還元公理の意義は、クラスに関してオーダーの区別を消去してくれること、言い換えれば、クラスに関しては外延性が成り立つことが保証されることである。こうして、クラスに関してはタイプの区別だけが問題となり、オーダーの区別を無視した非可述的定義が可能になる。しかし、これでは何のためにオーダーを導入したのか判然としない。ラッセルらは、還元公理が純粋にプラグマティックな正当化を持つとしているが、その導入を正当化する論証を欠いていた（Whitehead&Russell(1927),p.xiv;cf.Church(1956),§59.）。」
池田真治、伊藤遼、久木田水生「タイプ理論の起源と発展」,54p

「ゲーデルによれば、オーダーの理論は悪循環原理（VCP）に基づく。したがって、その批判は、VCPの厳密な分析によってなされる。VCPは、「いかなる全体も、その全体によってのみ定義しうるメンバーを含むことはできない」というものであった。そもそもVCPは、「定義によって導入される数学的対象は人間による構成と独立に存在するものではない」という構成主義的態度によって要請された。しかしVCPは、非可述的定義を認めず数学の大部分を破壊するため、要求としては強すぎる。全称量化を用いずに自然数を定義するには、ラムジーが提案したような無限連言による方法があるが、そこには無限の直観が入り込まざるを得ないとゲーデルは考えた。また、致命的なことに、オーダーの定義にはテクニカルな問題があって、自然数の帰納的定義に失敗しており、自然数が分岐タイプ理論から導出されるかすら明らかでない（G¨odel(1944),p.146）。そこでは、ラッセルは外延の同一性を担保に非可述的命題関数を容認しており、VCPを事実上放棄している。彼の数学的対象の存在に関する単一性の信念を支持するゲーデルにとって、一貫性を欠きまともに数学を展開できない以上、非可述性を避けるため概念に構成的階層を導くラッセルの立場は不合理に映ったのである。」

池田真治、伊藤遼、久木田水生「タイプ理論の起源と発展」,55p

内包的/外延的

内包､外延とは一体・・・？

すこし難しい話として､「内包的/外延的」という区別がある｡

三浦さんの説明によれば､「属性の表現法が違うと､その属性が従う論理が異なってくるような場合､その論理を『内包的』」と呼ぶらしい｡

正直､何を言っているかわからない｡「全ての事項が分からない」から､「全ての事項のうち､いくつかはわかる」へ､さらに「AとBとCが特にわからない」へ進めたらいいのだと思う｡とりあえずはどこが､どのようにわからないかを明らかにすることが「わかる」ための第一歩である｡だからこそ「わからなかったログ」も重要だろう｡

例:「鳥」の内包は、羽、翼、卵を産むなどの共通の特徴｡学者という概念の内包は「学問の研究者」である｡

例:「鳥」の外延は、ペンギン、雀、ワシなど、実際に存在する鳥の個体｡学者という概念の外延は､Aという医者､Bという医者である｡

1. 「属性の表現法が違うと､その属性が従う論理が異なってくる」場合､その論理を「内包的」という｡
2. 「個体を優先して命題の真偽だけを問題にする」場合､その論理を「外延的」という｡
3. ラッセルは個体よりも普遍を重んじ､「真偽の定まり方を問う」内包的論理を重視している｡

「現在医者として知られる全ての人物を列挙した集合のリストをつくる｡このリストにのっている人は医者である｡」というような外延的定義をラッセルはあまり重視していない､ということになるのだろうか｡

なぜなら､このような定義は集合や概念の本質的な「性質」に着目した定義ではないからである｡

・特に参考にしたページ
キーワード:内包､外延
三浦俊彦『ラッセルのパラドックス』,84-85p

属性の表現法が違うと､その属性が従う論理が異なってくる？

「属性の表現法が違うと､その属性が従う論理が異なってくる」場合､その論理を「内包的」というという説明は私にはまだ意味不明である｡

たとえば非述語的属性を述語的属性に還元すると､表現法が異なってくる｡この場合､属性が従う論理が異なる｡この論理というものが何を指しているか､私には意味不明である｡思いつくのはオーダーが異なるという点である｡「勇敢かつ・・好色かつ・・」というような論理形式と､「Aだけがもつ属性または・・・Bだけがもつ属性または・・・」といったものは「表現法」であり､それぞれが属するオーダー(論理)が異なると言ったほうがいいのかもしれない｡

といっても､AかつBやAまたはBのオーダーは同じであり､すべての・・・というような表現の違いがでてくると､その属性が従うオーダーが明確に変わりそうである｡あるいは「かつ」と「または」では相対的なオーダー差が対応していくと考えていくこともできるのかもしれない｡

論理形式は異なるが､しかし「共通の属性」について言及されているという点は同じである｡つまり､表現が異なると論理は異なるが､いずれも内包的である｡いずれも「属性」を重視している｡

例えるなら「医者である人々」よりも､「医者である人々がもつ性質」が重視されるのが内包的論理であり､また「医者である人々が持つ性質」を多様な表現で説明していることになる｡同じ値の異なる表現という点がポイントとなる｡同じ属性の異なる論理階型(=オーダー)と読み替えれば､論理形式が異なってくる､という意味合いがすこし理解できる｡

では､仮に外延的論理であった場合は､「表現が異なると論理が異なるということがない」ということになるのだろうか｡共通の性質というものをあまり考慮しないので､医者のリストさえ全て挙げることができれば､異なる表現というものが必要ないのかもしれない｡

つまり､表現法を多様にする(例えば述語的属性だけではなく､非述語的属性も取り入れる)ということにあまり意義を感じないのかもしれない｡それゆえに､外延的論理を重視する人達からすれば､内包的論理を重視する人たちは「余計な付け足し」だと思うのかもしれない｡

・特に参考にしたページ
キーワード:内包､外延
「属性の表現法が違うと､その属性が従う論理が異なってくるような場合､その論理を『内包的』という｡ラッセルの論理学は､個体を優先して命題の真偽だけを問題にする『外延的』論理ではなく､個体よりも普遍を重んじ､真偽の定まり方まで問う内包的論理であるため､正確に同じ項の集まりにあてはまる属性を別個のものとして区別することが必要になるのだ(同一の項たちにあてはまる属性を述語的と非述語的に区別するのはムダ､という批判をする論理学者は､クワインをはじめ､『内包的論理』の重要性を否定する人々である)｡」
三浦俊彦『ラッセルのパラドックス』,84p

世界を記述し尽くせるか

「結果的に完全な記述となっているだけでは足りず､その記述が完全な記述であるということも明示しているべきだ」

三浦さんによれば､ラッセルの論理学が内包的とならざるをえないのは「個別的事実で世界が記述し尽くせるとはラッセルは考えなかったから」らしい｡

たとえばラッセルは「『私が列挙したのは､宇宙の全ての個別的事実である』と付け加えない限り､あなたは宇宙の完全な記述をまだ成し遂げていないだろう」と述べている｡

たとえば無限のようにある「偉大な将軍に必要な属性」をひとつひとつ､述語的属性を全て列挙しつくせたと仮定する｡しかし､これでも「完全な記述」は完成しないという｡

なぜなら､「偉大な将軍に必要な属性を全てもっている」というような非述語的属性を付け加える必要があるからである｡あるいは「偉大な将軍に必要な属性はこれらの他に残っていない」というような非述語的属性でもいいのかもしれない｡とにかく､「非述語的属性が完璧な記述には必要だ」というのである｡もちろん､意味論的パラドクスを解決するために非述語的属性(オーダーの区別)が必要だという理由もあるのかもしれない｡しかしそのためだけだとしたらアドホック(その場しのぎ)だと批判されてしまう｡もっと根本的な導入の正当化が必要になる｡

非述語的属性は述語的属性に還元できるという前提があるのにもかかわらず､それでも必要なのかとラッセルを批判する人の気持ちが私にはわからなくもない｡

しかしベイトソンで私は「トートロジー(同義反復)を増やすことは蛇足ではなく､プラスアルファの理解のボーナスがあるという視点」を学んだので､仮に還元できたとしても異なる表現の重要さを理解することができる｡

「非述語的属性が完璧な記述には必要」ならば､「述語的属性と非述語的属性を区別するオーダーという考え方も必要」になるのだろう｡

したがって､「述語的属性だけでいい」という考え方にラッセルは同意できないということになる｡非述語的属性が述語的属性に還元できるからといって､不要とはならない｡世界の完全な記述は「結果的に完全な記述となっているだけでは足りず､その記述が完全な記述であるということも明示しているべきだ」というのがラッセルの考えらしい｡微妙なニュアンスの違いを理解することは難しい｡たとえばオセロをしていて､結果的､実質的に自分の駒のほうが多いとする｡しかし結果的に多いだけでは何となく足りない｡「自分の駒のほうが多い」と勝利宣言する必要がある｡この比喩が正しいかどうかはわからないが､私の理解はそういうイメージとなる｡

・特に参考にしたページ
キーワード:「非述語的属性が完璧な記述には必要だ」
「ラッセル論理学が内包的とならざるをえないのは､個別的事実で世界が記述し尽くせるとはラッセルが考えなかったからである｡『あなたが宇宙のすべての個別的事実を列挙し尽くすのに成功したとしても……『私が列挙したのは､宇宙のすべての個別的事実である』と付け加えないかぎり､あなたは宇宙の完全な記述をまだ成し遂げていないだろう』(論理学原子論の哲学)｡」
三浦俊彦『ラッセルのパラドックス』,85p

還元公理は「すべての哲学的議論で自覚されているべき仮定」である

他にも三浦さんは､還元公理が「すべての哲学的議論で自覚されているべき仮定」だと説明している｡これは興味深く､ひとつの重要なコード(鍵)となりそうである｡

述語/非述語の項目で､「美しい」という属性が述語的属性ではなく､非述語的属性を省略形で述べた可能性があることを学んだ｡このように､一見､述語的属性に見えるものも非述語的属性の可能性がある､ということを理解するために述語的属性/非述語的属性というオーダーの区別は重要である｡

そして､非述語属性を一端述語的属性に還元して議論しなおすということも重要であるという｡

たとえば「偉大な将軍が必ずもつ属性のうち､すくなくともひとつの属性をAさんもBさんも共有する」という文章があるとする｡しかしそれゆえに､AさんとBさんは似たような人物だ､とは必ずしも推論できない｡なぜなら､具体的にどの属性が共有されているか､上記の文章(非述語的属性)だけでは判断できないからだ｡

たとえばAさんは好色という属性をもち､Bさんは勇敢という属性をもつというようにオーダーをひとつ下げてから判断をすると､類似性を過大評価することがなくなりやすくなる｡

これはなかなかおもしろい｡「述語的属性への還元に備える」という姿勢が大事だということを学ぶことができた｡気づかないうちに､高オーダーだけで説明してしまっていて､何を意味してるかが曖昧で伝わりにくくなっていることがあるのは注意する必要がある｡意識的にはしごを登ったり降りたりする反復が大事であり､登っているのに降りたつもりになっているような混同をできるだけ避けるようにしたい｡結果的に同じことを意味しているとしても､コミュニケーションの受け手側の誤解しやすさには差があるだろう｡

・特に参考にしたページ
キーワード:「すべての哲学的議論で自覚されているべき仮定」
「『勇猛である』『好色である』……がすべてナポレオンにあてはまることを個別に述べ尽くしたとしても､『これらの他に､偉大な将軍に必要な属性は残っていない』と付け加えないと､ナポレオンの完全な記述は得られない｡つまり､『偉大な属性を”すべて”持っていた』といった非述語的属性は､述語的属性に還元できるからといぅて､不必要とはならない｡世界の完全な記述というのは､結果的に完全な記述になっているだけでは足りず､その記述が完全な記述であることをも明示しているべきなのだ！かくして､ラッセル的世界記述では､どうしても非述語的属性が持ち出されなければならないのである｡」
三浦俊彦『ラッセルのパラドックス』,85p

次回の予定､ベイトソンとの関連

次回の予定

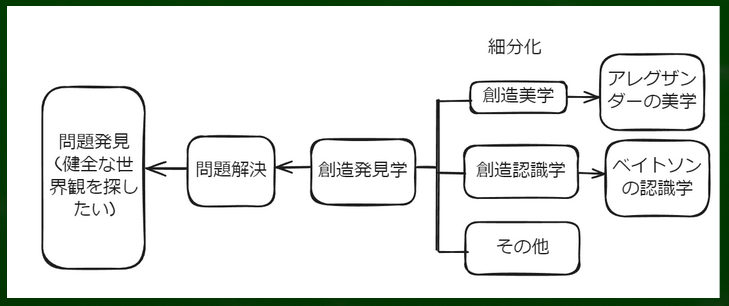
まず､大前提として､右の図のように今回の動画は創造発見学の一つのカテゴリーだという位置づけである｡そして一番根本的なカテゴリーだと考えている｡

・次回はベイトソンが論理階型理論をどのように用いているかを紹介していきたい｡すこしだけ先取りしておく｡

・ベイトソンは「論理の世界」と「現象(現実)の世界」の違いについて語っている｡

たとえば論理の世界は「無時間的」であり､現象の世界は「時間的」であるという｡たとえば論理の世界ではラッセルが行ったように発生したパラドクスは「なかったもの(最初から存在していないもの)」とされてしまうか､そもそも「生じないもの」という演繹体系を構築する｡しかし現象の世界では生じたパラドックスを「なかったものと」として葬り去ることはできない｡また､自己言及的なシステムが山ほどあるという点がポイントになる｡

ベイトソンは論理の世界と現象の「重要な違い」について語りつつも「重要な類似」についても語っている｡

その「重要な類似」が､「学習の現象」に論理階型理論のようなものが当てはまる」というものである｡たとえばタイプ０とタイプ１が区別されるように､学習０と学習１が区別されていく｡

また､ベイトソンの「ダブルバインド」という概念が論理階型の混同によって生じるという点も重要になってくる｡

次回はいきなり学習理論やダブルバインド理論を扱うのではなく､ベイトソンが考えた論理階型の混同の例を見ていくことにする｡

例えば「地図」と「土地」は違う､「鎖のつなぎ目が切れること」と「どのつなぎ目が切れるか」は違うなど､さまざまな論理階型の違いを学んでいく｡一通り学んだ後で､学習理論へ接続していき､さらにそこからダブルバインド理論へ接続していきたいと考える｡

「世界を二元化しない《精神》の定義は､どんな基準をもってすることができるのか｡」(グレゴリー・ベイトソン『精神と自然』125p)

精神の基準リスト

最後に､ベイトソンが考える精神の判定基準のリストを引用していく｡要するに､こうした基準をもっていれば､なんらかのシステムは精神と認められるというわけである｡たとえば思考､進化､エコロジー､生､学習などはこうした基準を満たすシステムでのみ起こるとベイトソンは考える｡それゆえに､認識論を考える前提として精神の基準リストを理解する必要がある｡

1. 「精神とは相互作用する部分(構成要素)の集まりである｡」
2. 「精神の各部分間の相互作用の引き金は､差異(ちがい)によって引かれる｡」差異とは時間上にも空間上にも位置づけられない非実体的な現象である｡差異はエネルギーにではなく､負のエントロピー/エントロピーに関係する｡
3. 「精神過程はエネルギー系の随伴を必要とする｡」
4. 「精神過程は､再帰的(あるいはそれ以上に複雑な)決定の連鎖を必要とする」
5. 「精神過程では､差異のもたらす結果を､先行する出来事の変換系(コード化されたもの)と見ることができる｡」変換のルールは比較的(すなわち変換される内容より)安定したものでなくてはならないが､それ自体変換を被ることもありうる｡
6. 「変換プロセスの記述と分類は､その現象に内在する論理階型のヒエラルキーをあらわす｡」

正直言って､最初にこれらのリストを単に見たとき､私には理解不能であった｡

そしてこのリストを一部でも理解するために､まず論理階型理論を理解しよう､というのが今回の動画の主な試みであった｡ベイトソンの主張だけでも理解できる人がいるかもしれないが､私の視点で異なる表現をすることによって､理解のボーナスが生じることを期待する｡

参考文献リスト

今回の主な文献

三浦俊彦「ラッセルのパラドクス: 世界を読み換える哲学 (岩波新書 新赤版 975)」

三浦俊彦「ラッセルのパラドクス: 世界を読み換える哲学 (岩波新書 新赤版 975)」

汎用文献

米盛裕二「アブダクション―仮説と発見の論理」

米盛裕二「アブダクション―仮説と発見の論理」

トーマス・クーン「科学革命の構造」

トーマス・クーン「科学革命の構造」

真木悠介「時間の比較社会学」

真木悠介「時間の比較社会学」

モリス・バーマン「デカルトからベイトソンへ ――世界の再魔術化」

モリス・バーマン「デカルトからベイトソンへ ――世界の再魔術化」

グレゴリー・ベイトソン「精神と自然: 生きた世界の認識論」

グレゴリー・ベイトソン「精神と自然: 生きた世界の認識論」

グレゴリー・ベイトソン「精神の生態学へ (上) (岩波文庫 青N604-2)」

グレゴリー・ベイトソン「精神の生態学へ (上) (岩波文庫 青N604-2)」

マックス・ウェーバー「社会科学と社会政策にかかわる認識の「客観性」」

マックス・ウェーバー「社会科学と社会政策にかかわる認識の「客観性」」

参考論文

・離散数学 | 植野真臣研究室 – 電気通信大学(URL)

・土屋盛茂「パラドックスとラッセルのタイプ理論」(URL)

・鈴木啓司「新たなる認識論理の構築14 : 集合論を超えて　境界についての認識論的考察」(URL)

・久木田水生「ラッセルの記述の理論とタイプ理論の関係について」(URL)

・池田真治、伊藤遼、久木田水生「タイプ理論の起源と発展」(URL)