創造法編集社

はじめに

動画での説明

・この記事の「概要・要約・要旨・まとめ」はyoutubeの動画の冒頭にありますのでぜひ参照してください｡

よろしければサイト維持のためにチャンネル登録をよろしくお願いしますm(_ _)mモチベになっていますm(_ _)m

バートランド・ラッセルとは、プロフィール

(パブリックドメイン,出典)

バートランド・ラッセル(1872-1970)はイギリスの哲学者であり､論理学者｡十九世紀末のイギリス経験論の断絶期に経験論を復興し､二十世紀初頭に集合論のパラドクスを発見して「数学の危機」をもたらし､その解決と「数学の論理学への還元」を目指した『プリンキピア・マテマティカ』を著したことで知られている｡

前提の記事

※創造認識学と創造美学は創造発見学のサブカテゴリーです

根本的な内容:創造発見学第四回:「創造発見学とはなにか」

前回の内容:創造美学第一回:クリストファー・アレグザンダーにおける「生き生きとした構造」とはなにか

記事の分割について

創造認識学第一回:「ラッセルのパラドクスの論理階型理論」とはなにか(前編)

創造認識学第一回:「ラッセルのパラドクスの論理階型理論」とはなにか(中編)

創造認識学第一回:「ラッセルのパラドクスの論理階型理論」とはなにか(後編)

記事が長すぎて重いので３つに分割することにしました｡動画では１つにまとめています｡

タイプ理論

単純タイプ理論

タイプ理論とはなにか､意味､定義､わかりやすく解説

追記:2024/07/14

たとえば悪循環原理に従うと「排中律」など大切な原理が意味をなくなるが､タイプ理論によって有意味なものとして認めることが可能になるという｡

タイプ理論は単純タイプ理論と､分岐タイプ理論に分かれる｡両者は共に､タイプやオーダーといった階型を導入することによって不都合を解消しようとする理論である｡

・特に参考にしたページ

キーワード:タイプ理論の説明

「タイプ理論は､悪循環原理に従いながらも､M2のような明らかに有意味な命題をきちんと命題として認めさせてくれる理論である｡」
三浦俊彦『ラッセルのパラドックス』
55p

単純タイプ理論とはなにか､意味､定義､わかりやすく解説

ベイトソンを学んでいると､ややこしい用語が出てくる｡それが「タイプ」と「オーダー」である｡この違いが私には全く理解できなかった｡

どちらも「階層(階級)」と日本語で表現できるものである｡

ざっくりいえば使われる文脈によって階層をタイプといったりオーダーといったりしているような印象を受ける｡

タイプ理論ではタイプが主に扱われ､分岐タイプ理論ではタイプと､同じタイプ(階層)の中でさらに異なるオーダー(階層)が扱われるというイメージである｡

・特に参考にしたページ

キーワード:単純タイプ理論の説明

「タイプ理論では､この世にあるものをすべて階層に分ける｡タイプ０､タイプ１､タイプ２､……というふうに｡」
三浦俊彦『ラッセルのパラドックス』,56p

集合におけるタイプ分け

具体例を見ていこう｡

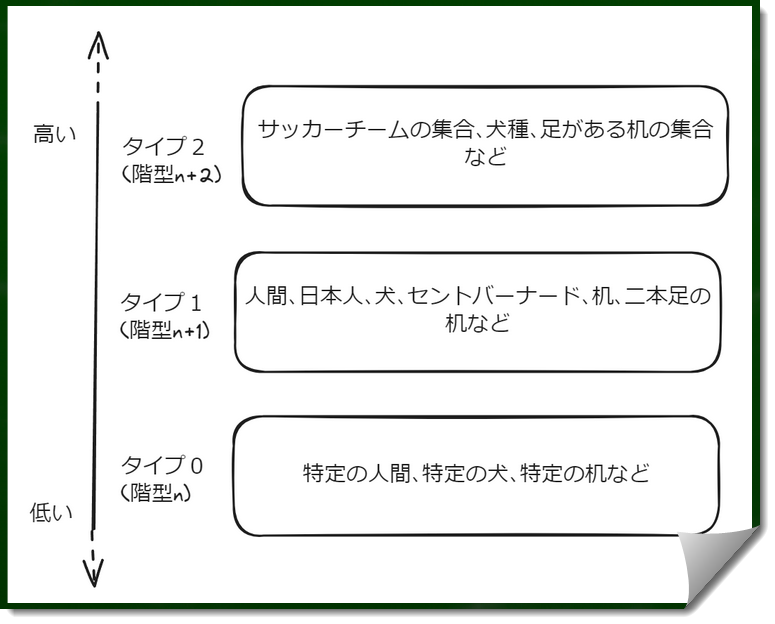
最下位のタイプ０は「個物」と呼ばれ､その「個物」の集合がより上位のタイプ１､「個物」の集合の集合がより上位のタイプ２､「個物」の集合の集合の集合がより上位のタイプ３・・というように階型が上がっていく｡

例えば「あの紙」より「紙」のほうが階型が高い｡

図にするとこのようなイメージとなる｡

※仮に特定の人間などを最小の個物とし､タイプ０と仮定した場合｡

・特に参考にしたページ
キーワード:集合におけるタイプ分け

「たとえば､あなたや私やあの犬､この猫､この机､そのボールペンなど､個物が一番低階層の『タイプ０』に属する｡次に､人類(個々の人間の集合)､犬一般(個々の犬の集合)､机一般(個々の机の集合)はひとつ上の『タイプ１』に属する｡タイプ１集合の部分集合､たとえば日本人､セントバーナード､白い机などといった集合や､合併集合､たとえば人間か犬であるものの集合､机かボールペンであるものの集合､といったようなものも､含む要素の範囲の広さが違うだけなので､同じくタイプ１に属する｡さらに､人間の集合の集合(たとえば､各国ごとの国民の集合､サッカーチームの集合､男と女という二つの要素から成る集合など)､犬の集合の集合(セントバーナード､マルチーズ､柴犬､ドーベルマンなどを要素とする『犬種』という集合)などは､タイプ２に属する｡」
三浦俊彦『ラッセルのパラドックス』,56p

性質におけるタイプ分け

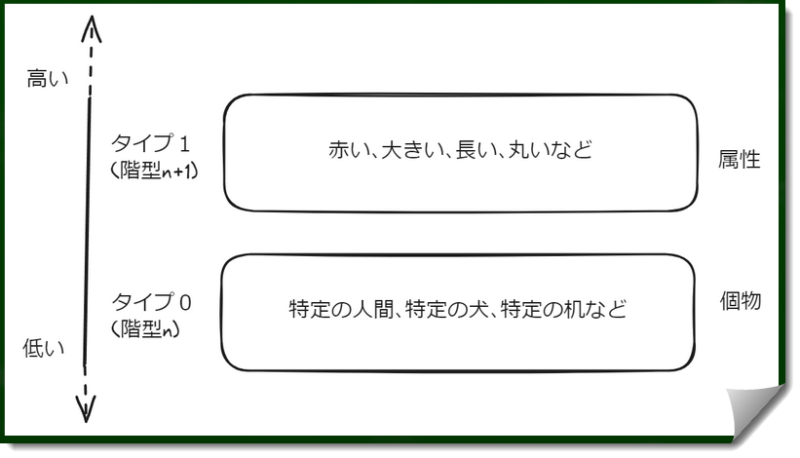
性質とは「個物がそれを持つかどうか問うことが意味をなすような属性」を意味する｡最下位のタイプ０である「個物」よりも､「個物がもつ属性である性質」のほうがタイプが上位である(タイプ１)｡

例:「赤い」という性質は､「赤い個物の集合」と同じレベルに位置している｡「あの紙」よりも「赤い」のほうが階型が高い｡では属性同士のタイプはどうなっているのか､という問題があるだろう｡この問題は後で扱う｡

図にするとこのようなイメージとなる｡

・特に参考にしたページ
キーワード:性質におけるタイプ分け

「集合についていま述べたタイプ分けは､性質についてもあてはまる｡まず､『赤い』『熱い』『大きい』『勇敢である』のような､個物にあてはまる性質(つまり､個物がそれを持つかどうか問うことが意味をなすような属性)はタイプ１である｡なぜなら､個物がタイプ０であり､赤い個物の集合はタイプ１であって､『赤い』という性質は赤い個物の集合と同じレベルに位置しているはずだからである｡」
三浦俊彦『ラッセルのパラドックス』,58p

要素の範囲の広さとタイプ分けの関連性

【ポイント】含む要素の範囲の広さが違うことが論理階型の違いをあらわすわけではない

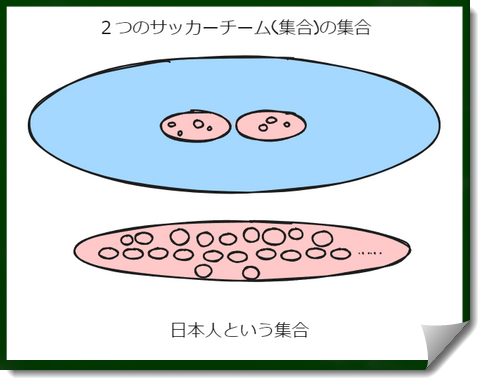
たとえば人類という集合も､日本人という集合も､犬という集合も､セントバーナードという集合も同じタイプ１に属すると考えることができる｡

比喩的にいえば横の広さではなく､縦の長さが重要になるということだろう｡要素の集合よりも､要素の集合からなる集合のほうが論理階型が高い｡

たとえば日本人のほうが､(たとえば東京都にある)サッカーチームという複数の集合からなる集合より人数は多く､(横の)範囲は広そうだ｡

いやいやそもそも人間も原子の集合であり・・いや細胞の・・・と言い出すこともできるかもしれない｡つまり､同じような概念でも集合の定義次第で論理階型の高低が変化する｡

どのようなタイプとみなすかは人それぞれ､というわけではない｡一定のルールがある｡しかしどこまでをクラスのサブクラス､あるいは個物と表現するかについては表現者の状況によるのだろう｡

原子や細胞レベルまで考える必要がない､という合理的な理由があればそれらをわざわざ一番低いタイプと明記して分析をする必要がないのではないだろうか｡

食べ物のサブクラスに果物､甘いもの､リンゴを置くのではなく､いきなりそのリンゴを置くというように表現(定義)することも可能だったことと似ている｡

しかしサッカーチームと日本人は同じ論理階型であり､日本人よりも複数のサッカーチームからなる集合のほうが論理階型が高い｡これを抽象化すれば､集合よりも､集合の集合のほうが論理階型が高い｡

・特に参考にしたページ
キーワード:含む要素の範囲の広さが違うこと

三浦俊彦『ラッセルのパラドックス』,55p

ある存在者のタイプは固定的(絶対的)か､流動的(相対的)か

ある存在がどのタイプかというのは絶対的で固定的なものではなく､相対的で流動的なものということになる｡

純粋な数理論理学からすれば､そんなものは知ったことではないとなるのかもしれない｡

例えばリンゴと日本人のどちらが論理階型が高いのか､と問われれば難しいだろう｡リンゴをあのリンゴなどの個物からなる集合､日本人をあの田中さんなどの個物からなる集合と安直に定義すれば､論理階型は同じとなる｡

論理学においては絶対的なルールがある｡それは要素よりも集合が､集合よりも集合の集合のほうが論理階型が高いというルールである｡論理学は具体的な内容を扱うというよりも､形式を扱う学問である｡

三浦俊彦さんの説明では「タイプ理論の骨子は､さまざまな存在者を相対的に異なったタイプに分離することなので､特定のタイプの絶対的な順位を突き詰めることは重要でない」とある｡

日本人や人類という概念をどのように考えるか､というのは論理学の範囲ではないのだろう｡「要素(個物)の集合」と「要素の集合の集合」という抽象的なクラスを比べた場合､必然的に後者のほうがタイプが高い､「項」よりも「属性」のほうがタイプが高い､論理階型の特定の組み合わせはナンセンスだといったことがとりあえずは重要なようである｡

追記:2024/07/14

・特に参考にしたページ
キーワード:タイプは相対的､体系的曖昧さ

三浦俊彦『ラッセルのパラドックス』,61p

項と述語とはなにか､意味､定義､わかりやすく解説

ラッセルは項と述語を以下のように定義している｡

【ポイント】項や述語のタイプは文によって変わる 

三浦さんの例では「たとえば『地球は青い』と言えば項は地球､述語は青だが､『青は色である』と言えば青は項として登場してくることになる｡項のタイプは､文によって変わってよい｡」という｡

・特に参考にしたページ
キーワード:項と述語の違い､流動性
「『個物』『属性』という言葉は､それぞれタイプ０､１に固定された存在者を指すように受け取られるが､相対的なタイプ差だけを示すためにラッセルは､タイプにかかわらず個物のようにふるまうものを『項』､項の持つ属性のようにふるまうものを『述語』と呼ぶ｡たとえば『地球は青い』と言えば項は地球､述語は青だが､『青は色である』と言えば青は項として登場してくることになる｡項のタイプは､文によって変わってよい｡ただし､項､述語というと言語表現そのものを指す文法用語のニュアンスがあるが､あくまでさまざまな存在者を指すので注意しなければならない｡」
三浦俊彦『ラッセルのパラドックス』,59p

文や命題の階型はややこしい

個物も属性も､存在者である

単純タイプ理論において､性質におけるタイプ分けというものを学んだ｡「個物よりも個物がもつ属性のほうがタイプが上位である」というルールである｡

たとえば「赤い」というのは「そのリンゴ」という個物がもつ属性であり､論理階型が１高い｡そして「赤い」は「赤い個物の集合」と論理階型が同じである｡

「個物」と「属性」はいずれも「存在者」である｡個物は具体的に存在し､属性は個物に付随する性質や特徴として抽象的に存在する｡

具体的にいえば「そのリンゴ」も存在者であり､「赤さ」も存在者である｡しかしこれらは「個物」と「属性」に区分して考えることができる｡それではペガサスという名前に対応する存在者は？という問題になると､フッサールの「無対象表象問題」とつながっていくので面白い(詳細はフッサール第一回の動画で説明)｡

【応用哲学第一回】フッサールの現象学における「志向性」とはなにか

命題は属性である

「存在者」を文章や命題によって表現する場合､話が複雑になってくる｡

まず大前提として､「命題」は個物ではなく､属性である｡つまり抽象的な存在である｡「S(主語)はP(述語)である」というのが基本的な命題である｡

具体的にいえば､「このリンゴは赤い」は命題であり､このリンゴは主語であり､赤いは述語である｡

三浦さんは「命題とは､現実世界を項とする属性として解釈できる」と説明している｡ここでいう現実世界とはナポレオン🧍であったり､りんご🍎であったり､あるいは赤さ🔴や果物🧺などを意味する｡つまり､あらゆる「存在者」を意味する｡「指示対象」ともいえるかもしれない｡

ということは､命題全体が指示するような「事態」もなんらかの意味で存在するのだろう｡このあたりはフッサールと関連が深そうだ｡ただし､ラッセルが事態についてどう考えていたか私にはよくわからないので､省略する｡「命題関数」などと関係がありそうな話だが､まずは保留する(後で少しだけ扱う)｡

1. 「このリンゴは赤い」は命題であり､属性である
2. 「このりんご」は「主語(項)」であり､属性である｡
3. 「赤い」は「述語」であり､属性である｡

このように､命題も属性であり､それぞれのパーツも属性であると言える｡

要するに､命題も主語も述語も「指示(表現)」に過ぎず､「指示対象そのもの」ではない｡「このリンゴ」は指示であり､眼の前にある🍎は「指示対象」である｡もちろん､🍎一般のような直接には目に見えない抽象的存在であれ､存在するのであり､指示対象になりうる｡

そして指示において､何が主語であるか､述語であるかは流動的である｡たとえば「地球は青い」ともいえるし､「青は色である」ともいえる｡それゆえに､「青い」という指示が固定的に「述語」として振る舞うわけではなく､「項」として振る舞うこともある｡要するに､同じ存在者を主語として扱ったり述語として扱っている｡

「このリンゴは赤い」という文章において､「このリンゴ」は個体のようにふるまうので「項」である｡つまり主語である｡「赤い」は属性のようにふるまうので「述語」である｡

しかし､「このリンゴ」という表現(指示)は個体ではない｡あくまで個体として振る舞っているに過ぎない｡たとえばメニューと実際の料理が違うのと似ている｡もしこれらを同じ次元で同一視すれば論理階型の混同になる｡

・特に参考にしたページ
キーワード:命題のタイプについて
「前章で､排中律に則して『命題の階層』を見たが､ここで改めて正確に言い直すと､命題の階層は､実はオーダーである｡命題とは､現実世界を項とする属性､として解釈できるからだ｡命題『人間は死ぬ』は､現実世界にあてはまる述語的属性である｡命題『人間は死ぬというのは真である(真なる命題すべての中に『人間は死ぬ』が含まれる)』は､第２オーダーの属性である｡……等々｡どの命題も､同じ現実世界を項とする属性なので､命題にタイプの区別はないのである｡」
三浦俊彦『ラッセルのパラドックス』,80p

単純タイプ理論を用いて命題の要素をタイプ分けしてみる

単純タイプ理論のみを用いて区別してみよう｡

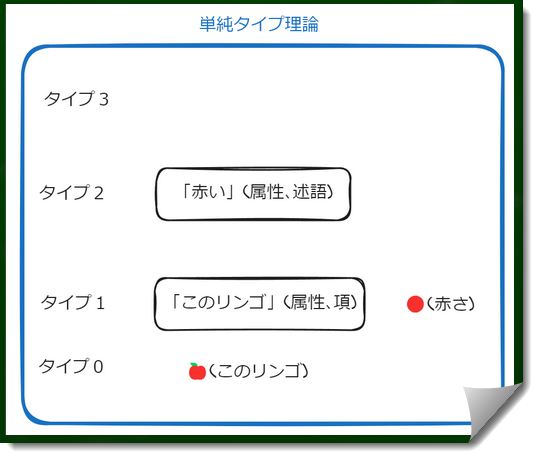この🍎は個物であり､タイプ０である｡「このリンゴ」は「個物を指示する表現」であり､タイプ１である｡🔴(赤さ)は属性であり､タイプ１である｡「赤さ」は「属性を指示する表現」であり､タイプ２である｡

ここで困るのは､命題をいかなるタイプにするべきかという点である｡私はタイプ３になるかと思っていたが､どうやら単純タイプ理論ではそうではないらしい｡

まず､「赤い」がタイプ２なのはタイプ１への言及だからである(タイプ１という項がタイプ２という述語をもち､述語の方が階型が高くなければならない)｡仮に「このリンゴは赤い」という命題がタイプ２よりも上位なら､タイプ２自体への言及がどこかに含まれている必要がある｡もし命題が項であるなら､いずれかの「存在者(指示対象)」への指示であり､このいずれかの存在の階型がポイントとなるだろう｡

純粋に､現実の存在である赤さがタイプ１であり､このリンゴがタイプ０なので､それらへの言及と考えてタイプ２と考えてもいいかもしれない｡あるいは命題内のパーツで一番高いタイプが２だから､という理由付けも考えたが､すこしスッキリしない｡

タイプ１とタイプ０の関係をあらわす関数として､タイプを１高くすると考えればタイプ２だというのは少しスッキリする｡あるいはタイプ０とタイプ１からなる「事態」なるものが実在すると考え､この実在をタイプ２に置けば事情は変わるのかもしれない(これだとタイプ３になってしまうが)｡

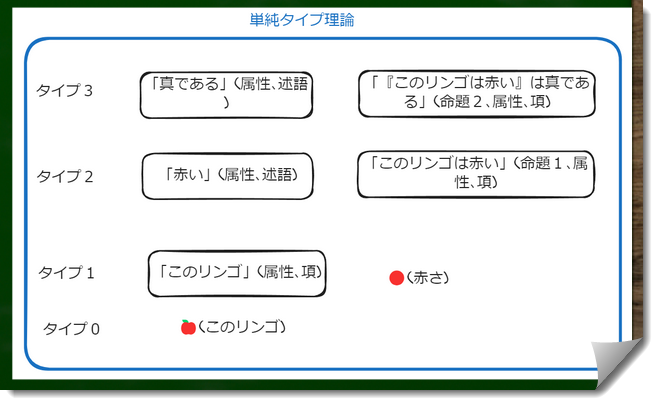「AはBである」に対してさらに何か言及があるとすれば､その言及はタイプ３となる｡つまり､「真である」はタイプ３となる｡

たとえば「この林檎は赤い」という命題がタイプ２であるとすれば､『「このリンゴは赤い」は真である』という命題と「真である」という属性はタイプ３となる｡

三浦さんはある場所で「正確には､命題の階層はタイプではなくオーダーに属するが､説明の都合上､真理を項-述語関係でシュミレートして､当面はタイプとして扱わせていただく」と説明している｡

ここが頭が混乱するポイントなのだが､いったいどういうことか｡そもそも意味論的パラドクスは単純タイプ理論では解決できないから､分岐タイプ理論が必要になったという理解を私はしていた｡ということは､三浦さんは実質的には分岐タイプ理論で説明しているが､単純タイプ理論風に記述しているということか､あるいはたまたま単純タイプ理論でも解決できるような単純な意味論的パラドクスなのか｡まずは三浦さんがシュミレートしたという「嘘つきのパラドクス」を見ていこう｡その後で､分岐タイプ理論でも説明してみよう｡

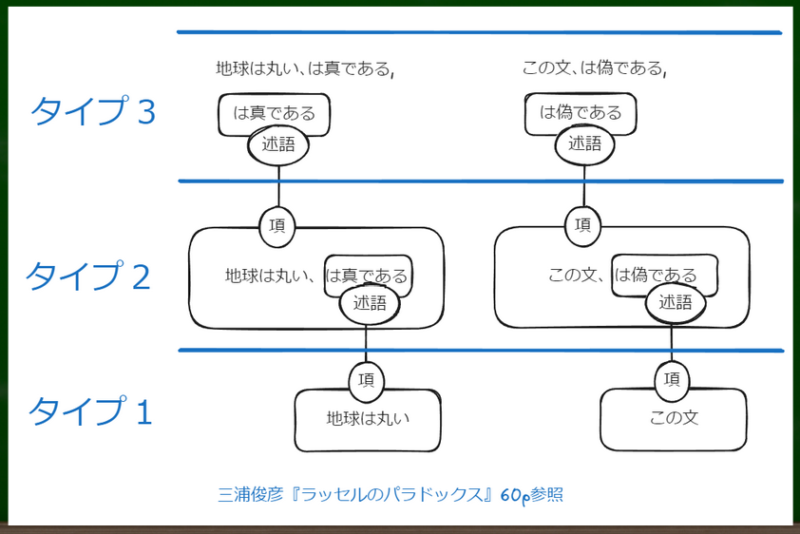
追記(2024/07/14):「私はタイプ３になるかと思っていたが､どうやら単純タイプ理論ではそうではないらしい」というのは､三浦さんの嘘つきのパラドクスにおけるタイプ分けに(単純タイプ理論)おいて､タイプ１に「この文」が､タイプ２に「この文は真である」が置かれていたからである｡

・特に参考にしたページ
キーワード:三浦さんの嘘つきのパラドクスにおけるタイプ分け
三浦俊彦『ラッセルのパラドックス』,60p

嘘つきのパラドクス

嘘つきのパラドクスとはなにか､意味､定義､わかりやすく解説

たとえば「この文は偽である」というような嘘つきのパラドクスを考えてみる｡もしこの文(「この文は偽である」)が偽であった場合､「この文は偽ではない」ということになる｡つまり､この文は正しい(真である)｡この文が正しい場合､「この文は偽である」ということになる｡

つまり､「この文は偽ではない」と同時に「この文は偽である」というパラドクスが生じてしまっている｡

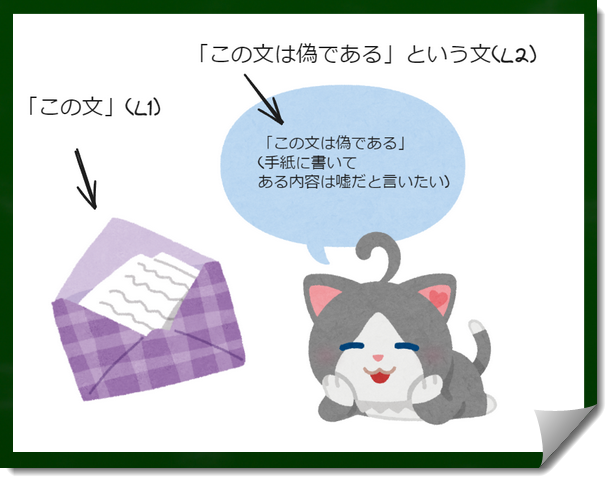
たとえば近くに手紙があるというような状況で「この文は偽である」と言われた場合､我々は偏屈でもない限り､それが指示している特定の文章が偽のことを書いてあるんだな､と思うだろう｡

イメージとしてはこれら２つの反応のうち､どちらかになる｡

嘘つきのパラドクスをタイプ分けする

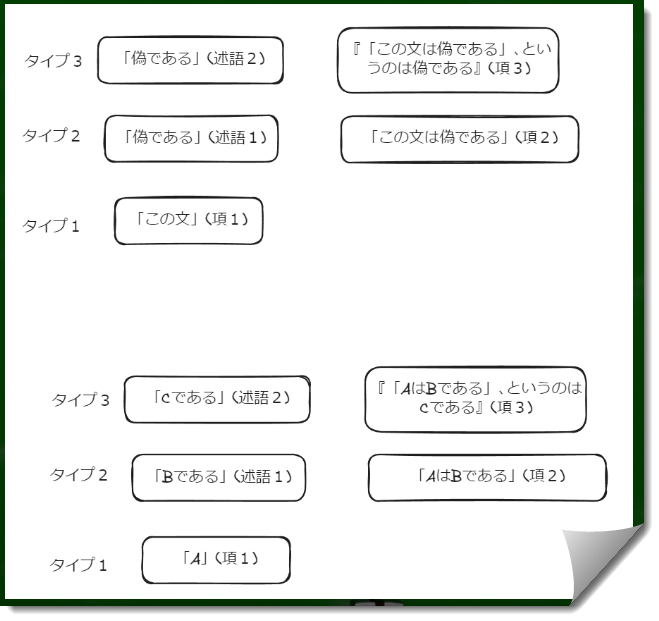
「この文」は個物のようにふるまうので項(主語)であり､「偽である」は属性のようにふるまうので述語である｡

従って､「この文」をタイプ１とすれば､「偽である」はタイプ２となる｡ここまではいい｡では､上記のように考えると「この文は偽である」という命題(項)はタイプいくつか｡

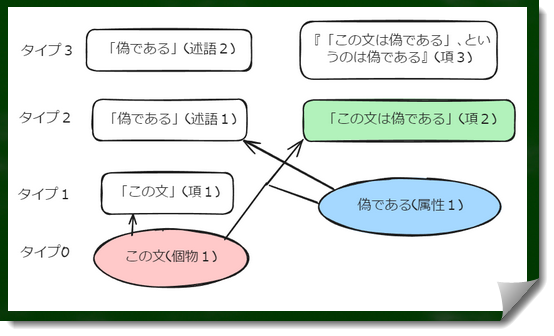結論から言うと､先ほど検討したように「この文は偽である」という命題(項)のタイプは２である｡

なぜなら､この命題は「この文(個物)」というタイプ０と「偽である(属性)」というタイプ１の関係からなる､より上位のタイプ１の項目であると仮定することができるからである｡

図にするとこのようになる｡

タイプ３の「偽である」とタイプ２の「偽である」は一見､同じ属性に見える｡しかしその属性を持つ項のタイプが違う｡

タイプ２の場合はタイプ１の性質であるから+１されたものとなり､タイプ３の場合はタイプ２の性質であるから+１されたものとなるという違いがある｡

嘘つきのパラドクスのタイプ分けの結論

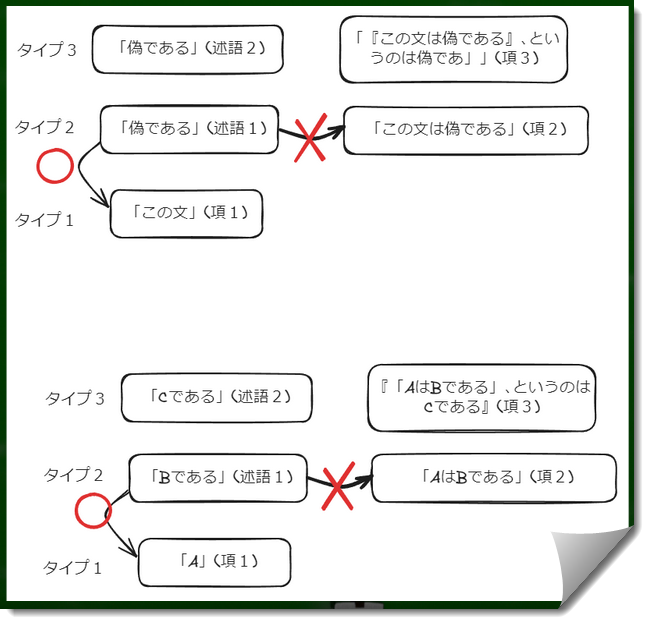
「この文は偽である」という文章を解体とすると「この文」(タイプ１､項)と「偽である」(タイプ２､述語)となる｡従って､「偽である」という性質はタイプ１の項に対して向っている｡

タイプ２の「偽である」が､タイプ２である「この文は偽である」という項の性質となることはできない｡もしそれが可能ならパラドクスになりうるが､しかしタイプ理論により､同じタイプ同士では主語述語関係を結ぶことはできず､無意味な文章となる｡AはBであるといっているのに､勝手にA+BはCであると解釈してはならない｡

「この文は偽である」という文章は､「(タイプ１に属する)この文は､偽である」と読み替えることができる｡

つまり､階型を限定する､はっきりさせるというテクニックによってパラドクスが解消される｡

・特に参考にしたページ
キーワード:三浦さんの嘘つきのパラドクスにおけるタイプ分け
「しかしタイプ理論では､『この文は偽である』の中の『この文』がLのことだとしたら､『この文は偽である』全体はLを指すことができない｡なぜならば､述語は項よりもタイプが上なので､さ「……は偽である」という述語を『この文』という項にあてはめた結果は､必ず『この文』という項にあてはめた結果は､必ず『この文』より高いタイプとならざるをえないからである｡こうして､『Lは偽である』は､名づけるとしたらLとは別の名､たとえばL２という名で呼ばなければならない｡L２が自分自身とは別の文Lについて『Lは偽である』と述べることには､なんの矛盾もないのである｡」
三浦俊彦『ラッセルのパラドックス』,60p

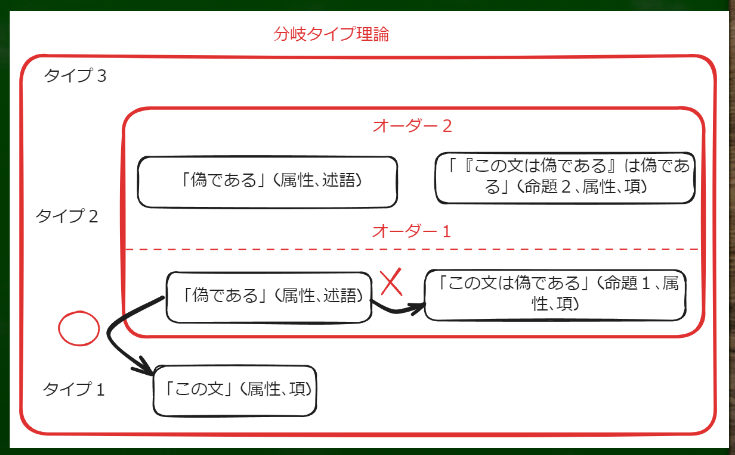
嘘つきのパラドクスを分岐タイプ理論で扱うとどうなるか

さて､問題はこれらを分岐タイプ理論で表現するとどうなるのかという点である｡分岐タイプ理論は後で扱うのだが､先取りしておく｡

1. 分岐タイプ理論では「属性に対してオーダーを設ける」という方法をとっている｡
2. 命題自体にタイプの区別はない｡

例えば分岐タイプ理論で「AはBである」という命題のタイプとオーダーを考えるとする｡

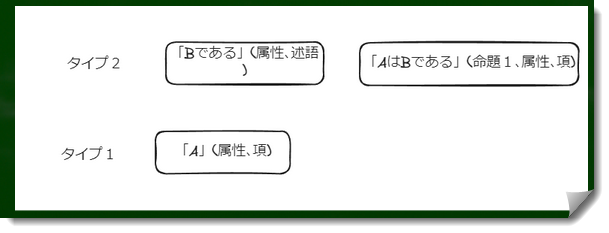
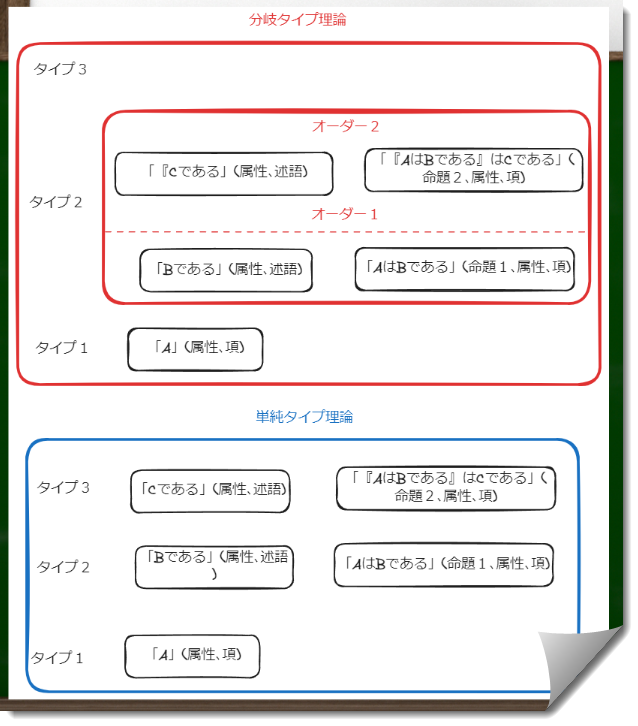
Aは項であり､タイプ１である｡Bは述語であり､タイプ２である｡「AはBである」もタイプ２である｡ここまでは単純タイプ理論と同じである｡※現実世界のタイプ分類は省略している(タイプ０に個物､タイプ１に属性などがくる｡)

しかし､分岐タイプ理論では「『AはBである』はCである」という命題はタイプ３に属さない｡「AはBである」はCであるという命題は､タイプ２の､第二オーダーに属する｡「AはBである」という命題は､タイプ２の､第一オーダーに属することになる｡

では､「Cである」という属性はどこに属するのか､という疑問も生じる｡順当に考えれば､タイプ２に属するのだが､タイプ２のどこに属するのか､正直判断に困る｡私はオーダー２に置かれると考えている｡

CはAやB､そしてAはBであるに対する言及なので､それより高い「階層(階型)」にある必要がある｡しかし､タイプ３にくるのはおかしい｡なぜなら､タイプ２のオーダー２にCがすでにあるからである｡従って､タイプ２のオーダー２にくるのが適切である｡

図にするとこのような違いとなる｡

要するに､A以外のあらゆる属性は同じタイプに位置し､そのタイプ内でオーダーが分かれるというわけである｡

嘘つきのパラドクスをあてはめてみると､上の図のようになるだろう｡

オーダー１同士で組み合わせることはできない｡したがって､「この文は偽である」という文章における「この文」が､「この文は偽である」という文を指すという解釈はできない｡

「この文」は先程の絵で言えば､手紙に入っている文章(L１､タイプ１)であり､「この文は偽である」という文章(L2,タイプ２のオーダー1)を指すのではない｡

三浦さんが単純タイプ理論でシミュレートしたという図を参考に作成し､引用しておく｡

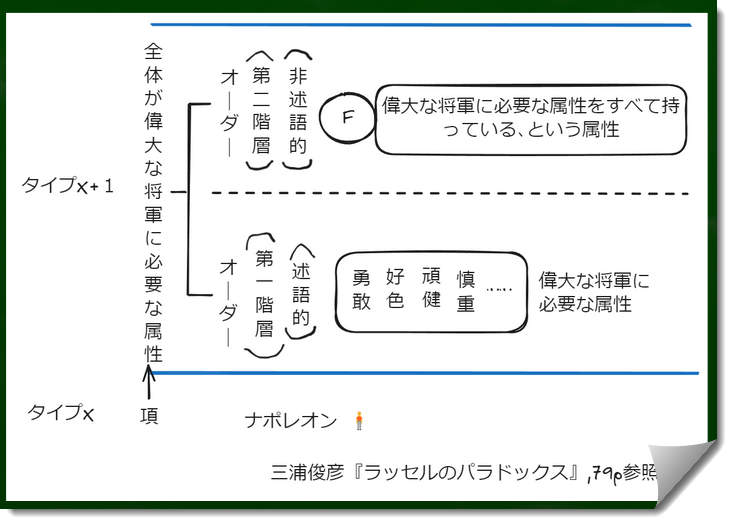
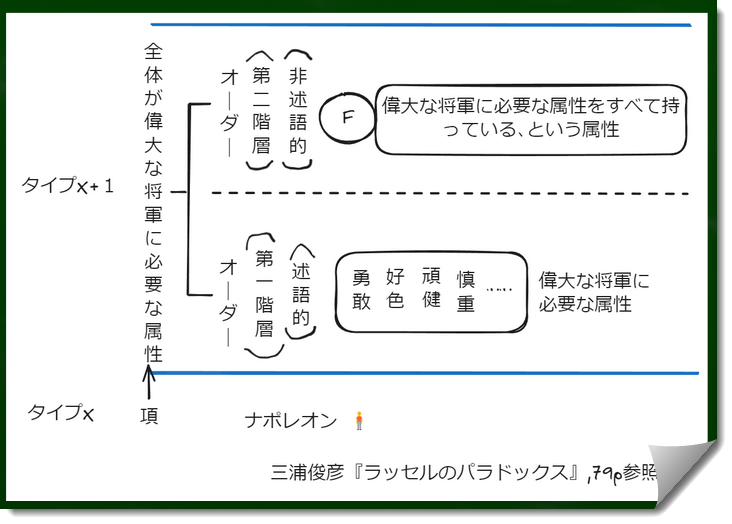
三浦さんは分岐タイプ理論の図の例も出しているのでこちらも引用しておく｡「ナポレオンは､偉大な将軍に必要な(第一階層の)属性をすべて持っていた」というような文のケース｡こちらは単純タイプ理論ではシミュレートできないような､複雑なケースなのだろう｡

ナポレオンの場合はタイプXはタイプ１であり､実在したナポレオン(現実の項)をタイプ０とすることができるのだろう｡

もし「将軍は､偉大な将軍に必要な・・・」と文章を変えれば､タイプXはタイプ２であり､オーダーが分かれるタイプは３であるということができる｡

ところで､「『AはBである』はCである」という第二オーダーの命題は､「非述語的属性」か､と私は疑問が生じる｡後で非述語的属性とは何かを考えていく｡

分岐タイプ理論

分岐タイプ理論とはなにか､意味､定義､わかりやすく解説

ラッセルはなぜ新たな理論を作る必要があったのか｡単純なタイプ理論だけでは「悪循環原理」を実現できないからだという｡単純タイプ理論で「論理的パラドクス」は解消できたが､「意味論的パラドクス」が解消できないという問題が生じたということである｡

分岐タイプ理論で「意味論的パラドクス」も解消できた｡しかしさまざまな問題が生じたという(数学に制約を課しすぎるなど)｡問題の解消のため､「還元公理」というものをラッセルは導入する｡しかしこの公理を導入することでもさまざまな問題が生じたという(批判も多い)｡結局､ラッセルは「還元公理」を縮小する形になったいう(どういう形か､私にはよくわからない)｡

まずは単純タイプ理論だけでは解決できないような意味論的パラドクスとはなにか､という問題を見ていく｡

この問題はポアンカレによって批判されたらしい｡

たとえばラッセルは「ベリーのパラドクス」といわれている問題をとりあげている｡

・特に参考にしたページ
キーワード:分岐タイプ理論
「つまりタイプ理論は､タイプとオーダーという､２つの次元に沿った階層区分を備えた体系なのである｡これまでナポレオンについて例を出してきたが､項をナポレオンではなく『将軍であること』とすれば､１タイプ上の項-属性関係が論じられ､そのタイプの中でまた､最低位オーダーの属性､次のオーダーの属性…等々が論じられることになる｡これが『分岐タイプ理論』だ｡各タイプが無数のオーダーに分かれることから､分岐と呼ばれる(逆に､各オーダーがタイプに分かれるとみなすこともできる)｡各タイプの中で､基本的な属性､つまり最もオーダーの低い属性を､ラッセルは『述語的』と名づけた｡第一オーダーの属性はすべて述語的である｡」
三浦俊彦『ラッセルのパラドックス』,79-80p

ベリーのパラドクス

ベリーのパラドクスとはなにか､意味､定義､わかりやすく解説

「一九字以下で名づけられない最小の自然数」という文章自体が十九字であり､名付けることができてしまっているという奇妙な事態をどう考えていくかが重要になる｡こういうパラドックス的な文章を考える度に私は頭がモヤモヤしてしまう｡

最小の自然数をaとする(このaは名前ではない)｡aは19文字以下で名付けることができないが､19文字以下で名付けることができてしまっている｡これは矛盾(パラドクス)である｡

「名付ける」というのは認識と対象の関係を含んだ心理的な概念であり､数学や論理学の範囲外だとラムジーに批判されていたそうだ｡こうしたパラドクスを特に「意味論的パラドクス」という｡嘘つきのパラドクスにおける「嘘」も同様なのだろう｡更に重要なのは､このベリーのパラドクスが単純タイプ理論によって解消できないという点である｡

・特に参考にしたページ
キーワード:ベリーのパラドクス
三浦俊彦『ラッセルのパラドックス』,74p

池田真治、伊藤遼、久木田水生「タイプ理論の起源と発展」,53p

単純タイプ理論でベリーのパラドクスを考える実験

(1)一九字以下で名づけられない最小の自然数の集まりは､例えばどのようなものがあるか｡たとえば３０文字で名づけられる最小の自然数があると仮定してみる｡

ここでは３０文字で「せんにひゃくさんじゅうよんまんごせんろっぴゃくななじゅうはち」と名づけられる自然数12345678だと仮定する(適当に仮定しただけ)｡「せんにひゃくさんじゅうよんまんごせんろっぴゃくななじゅうはち」は名前である｡したがって､名づけられた当の数字(自然数a)よりも論理階型が高い｡

(２)「せんにひゃくさんじゅうよんまんごせんろっぴゃくななじゅうはち」という名前をメンバーとして持つ､クラス(集合)がある｡これが「一九字以下で名づけられない最小の自然数」というクラスである(名前ではない)｡

クラスはメンバーの一員となることはできない｡したがって､「一九字以下で名づけられない最小の自然数」というクラスに「せんにひゃくさんじゅうよんまんごせんろっぴゃくななじゅうはち」というメンバーは入ることができるが､「一九字以下で名づけられない最小の自然数」というクラスは入ることができない｡

悪循環理論に反しているから自己言及的なクラスを認めない(名前の全体などというものはない)と仮定しても問題が生じる｡

例えば自然数aをnタイプ､「せんにひゃくさんじゅうよんまんごせんろっぴゃくななじゅうはち」という名前をn+1タイプとする｡

そしてn+1タイプである「せんにひゃくさんじゅうよんまんごせんろっぴゃくななじゅうはち(x)」に対する言及として「(xは)一九字以下で名づけられない最小の自然数である」という述語を考える(「その名前は１９文字以下である」と限定する言及のイメージ)｡この場合､タイプn+1に対する言及なので､その言及はタイプn+2に属することになる｡

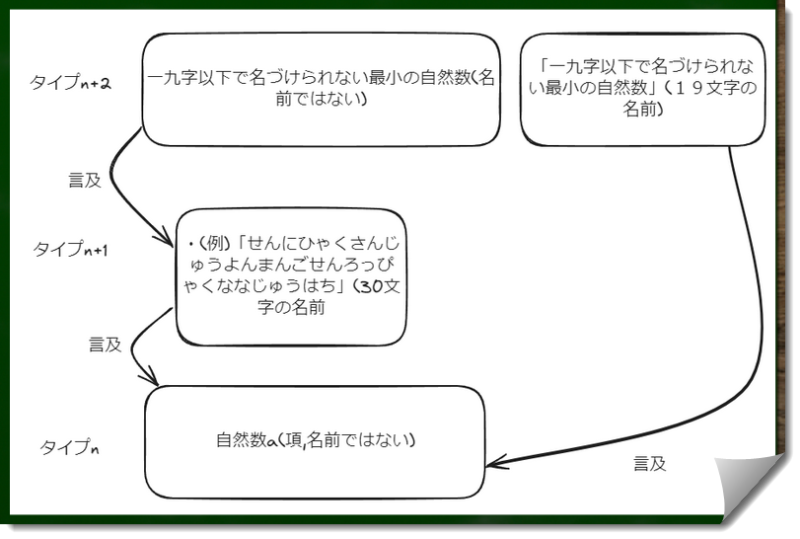
単純タイプ理論で分けて考えると､このような図になるだろう｡

なぜ「十九字以下で名づけられない最小の自然数」という述語と､「十九字以下で名づけられない最小の自然数」という項目が同じタイプn+2に位置するのか｡

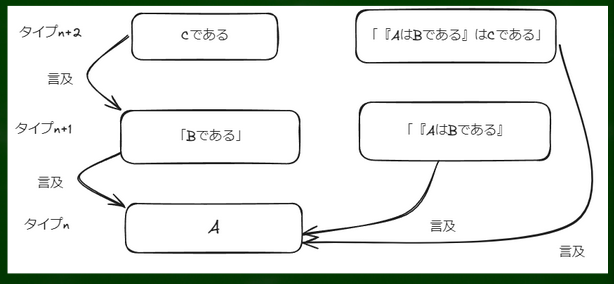
AとBとCのような記号で考えるとわかりやすい｡CであるはBであるに対する言及であるから､タイプが１高い｡そして「一九字以下で名づけられない最小の自然数」という名前はcを内部に含むものであり､cより下のタイプに属しているのはおかしい｡したがって､n+2タイプに属する｡正直このあたりの理屈はいまいちわかっていない｡

しかし､ここで問題が生じる｡

タイプnの自然数aに対する名前は全てタイプn+１に属するべきである｡このタイプn+1を仮にm+1とする｡

m+1=n+1=n+2となってしまい､おかしい｡要するに､タイプnに対する言及である名前は､タイプn+1に来ているはずであるのに､タイプn+2に一部が来てしまっている｡後で検討するように､仮にn+2に属している「十九字以下で名づけられない最小の自然数」という名前を､単にn+1に移動しただけでは問題は解決しない｡

・特に参考にしたページ
キーワード:タイプnの自然数aに対する名前は全てタイプn+１に属するべきである
「さてしかし､ベリーのパラドクスのこの解決で用いられた『階層』の区別は､『タイプ』の区別ではないことは明らかだろう｡十九字以下で名づけられない最小の自然数をaとし(念のため､『a』は名前ではありません)､あが十九字以下で名づけられないという場合の(たとえば三十字による)名づけがタイプnにおいてだとすると､『十九字以下で名づけられない最小の自然数』という名前は､タイプn+1に属していなければならない｡しかし､その両方ともが､同じ自然数aに対する名づけなのである(タイプnの場合は三十字の名づけ､タイプn+1の場合は十九字での名づけ)｡しかしこれはおかしい｡自然数aがタイプmの存在者だとすると､自然数aの名前は､タイプm+1であるはずだ｡すると､右の二つの名前の階層について､m+1=n+1でなければならない｡これは不合理である｡となると､名前の階層は､同じ項aよりも１タイプ上のタイプの内部で分かれているような階層でなければならない｡」
三浦俊彦『ラッセルのパラドックス』,76p

分岐タイプ理論でベリーのパラドクスを考える実験

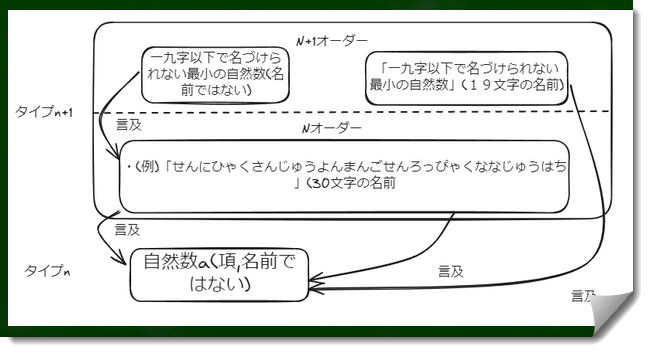
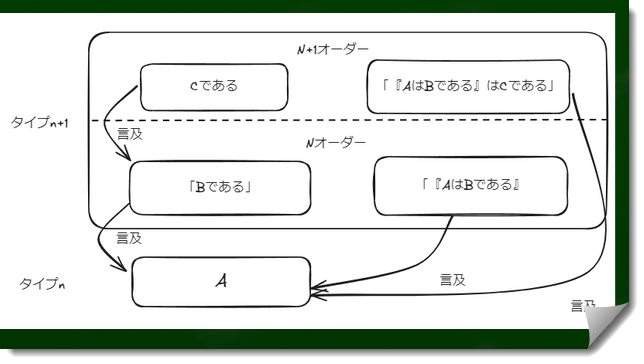
単純タイプ理論における問題を解消するために､分岐理論ではタイプ１の内部で階型(オーダー)を考えていく｡Cであるという述語がBであるという述語よりも高いオーダーであり､また「『AはBである』はCである」は「AはBである」よりも高オーダーであると考えていく｡

そうすれば､タイプnの名づけは全てタイプn+1に属するという点でスッキリする｡つまり､タイプm+1=n+1となり､不都合は生じなくなる｡こうした不都合をなくしたうえで､特定の階型に限定した言及と見なすという作業を行っていくことになる｡

・図にするとこのようなイメージとなる

ラッセルは『「一九字以下で名づけられない最小の自然数」は何だろう』という文章の中に､ある但し書きが常に隠れていると見なさなければならないという｡

但し書き:「第n階層(オーダー)の名前で名づける」

オーダーという概念を体系に導入し､このような但し書きが隠れているとみなせば､パラドクスは解決する｡

・特に参考にしたページ
キーワード:第n階層(オーダー)の名前で名づける
「『プリンキピア』でのラッセルの診断はこうである｡『十九字以下で名づけられない最小の自然数』という名前は､『名づけられる』という限定によって､名前でありうるものの全体に暗に言及している｡しかし自分自身がその全体の一要素なので､悪循環原理に違反している｡よって､名前の全体などというものはないのであり､いろいろな名前は階層に分かれているとしなければならない｡つまり､『第n階の名前で名づけうる』というような但し書きが常に隠れていると見なさねばならない｡そうすれば､『十九字以下で名づけられない最小の自然数』という名前そのものは､『名づけられない』とされた範囲外の一階層上の名前なので､それ自体が十九字以下であっても､その名の指定する性格づけとは矛盾は生じないのである｡」
三浦俊彦『ラッセルのパラドックス』,74-75p

オーダーを区別することで結局なにが変わったのか

『「(n+1オーダーの名前で名づける)一九字以下で名づけられない最小の自然数」は何だろうか』と解釈できるようになったのである｡

n+1の名前は(例えば)「せんにひゃくさんじゅうよんまんごせんろっぴゃくななじゅうはち」が選ばれることになる｡「一九字以下で名づけられない最小の自然数」という名前がより上の階層の名前となり､選ばれる範囲に含まれなくなる｡これでパラドクスが解消されるというわけである｡

両方の範囲が同時に選ばれうるような理論だと､問題が生じてしまう｡

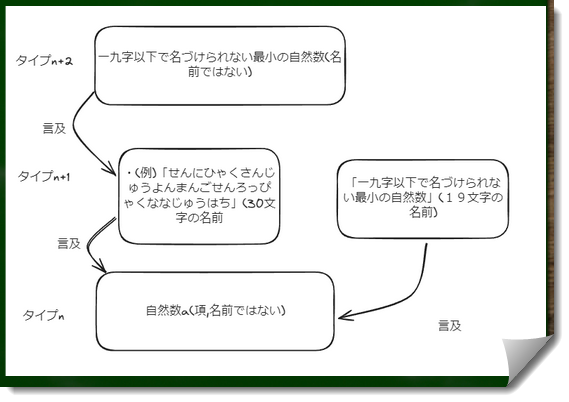例えばこのように単純タイプ理論で考えてしまうと､確かに名前はn+1の階層で全て収まっている｡しかし１９文字以下であり､かつ２０文字以上である(１９文字以下ではない)名前で名づけられる自然数aというものが存在することになってしまう｡そんな自然数aは､おそらくないだろう｡

命題関数

命題関数とはなにか､意味､定義､わかりやすく解説

属性は「１項関係」とも呼ばれる｡

たとえば「あの空は青い」というときの「あの空」は個物を名指すもの(項,主語)であり､「青い」は属性を名指すもの(述語)である｡

「xは青い」というような変項(空欄)を含む枠組みをラッセルは「命題関数」と呼ぶ｡

「あの空は青い」というように､変項に具体的な個物を代入すれば「命題」(真偽が判定可能な文)となるからである｡

事態と命題関数､そして命題との関連性はよくわからない｡今回はあまり触れない｡

「xはyよりも青い」という文章では変項が２つある｡この場合は「２項関係」となる｡変項が１つの場合をラッセルは属性ではなく「１項関係」と呼んでいる理由は､ラッセルが属性よりも関係を命題関数の本性だと考えたからだそうだ｡

２項以上の関係は､それぞれの属性間の関連性を示すという点が重要となるのだろう｡「xとyは青い」は２項以上だが､しかし実際は「xは青い」､「yは青い」と言っているに過ぎないのだろう｡「xよりyのほうが青い」という場合は､さきほどのような分割はしにくい｡

・特に参考にしたページ
キーワード:命題関数

「『xは死ぬ』『xは人間である』『xはyの父親である』『xはyにzを与えた』のように､空欄(変項)を含む枠組みを､ラッセルは『命題関数』と名づけた｡変項に具体物(項)を代入すれば命題となるので､項から命題への関数､とうわけである｡変項が一つの場合を『属性』と呼び､n個以上の場合を『n項関係』と呼ぶのが普通だが､総括的に捉えるためにラッセルは属性を『１項関係』と見なし､属性よりも関係こそが命題関数の本性だと考えた｡」

三浦俊彦『ラッセルのパラドックス』,66p

我々が名付ける前にはどのような世界が広がっているのか

たとえば「このリンゴは赤い」というのは命題である｡その命題を生み出したであろう「なにか」が眼の前にほんとうにあるのか｡「このリンゴ」という属性(項)だけにしぼったとしてもやはりそれを生み出した「なにか(個物)」､「それ」があるのか｡「このリンゴは赤い」から「このリンゴ」を抽出する作業は全体から引き算をしてなにかをとりだすようなイメージなのかもしれない｡我々が名付ける前にはどのような世界が広がっているのか｡ラッセルはこれに関して「センスデータ」を語るのだが､今回は省略する｡

これはフッサールの「感覚与件の謎」ともつながる､思ったより深い問題(存在論)なのだろう｡ハイデガーならそれは学問の対象にすることが難しい､贈与されたものだというかもしれない｡ベイトソン的にいえばなんら体系をもたない､関係しないような独立した個物のようなものを想定することは難しいというのだろう｡差異がなければ我々に情報として届かず､差異は２つ以上の個物の関係から生じるからである｡

述語的/非述語的

述語的属性とはなにか､意味､定義､わかりやすく解説

文章において何が項になるのか､述語になるのかは固定的ではなく､流動的であることを学んだ｡

・基本的な属性であり､「可述的」と表現されることもある｡

例:赤い､人間である､美しいなど｡

・特に参考にしたページ
キーワード:述語的属性

「ナポレオンについていえば､述語的属性とは､『頑固である』『人間である』『癌で死んだ』等々､私たちが基本的と認める『普通の性質』のことだ｡先ほどの､『偉大な将軍に必要に必要な属性をすべて持っていた』のような､オーダーの高い属性は､いかにも普通ではない､基本的ではない属性のように思われるだろう｡そういう属性は『非述語的』である｡」
三浦俊彦『ラッセルのパラドックス』,81p

「しかしたいていの非述語的属性は､述語的属性に還元されたとき､その表現法は､日常言語の表現とは似ても似つかぬものになっていなければならない｡一般には､多くの述語的属性の複雑な組み合わせ(先ほどのGのような)によって表現されなければならないことになるだろう｡」
三浦俊彦『ラッセルのパラドックス』,84p

非述語的属性とはなにか､意味､定義､わかりやすく解説

基本的ではない属性であり､「非可述的」と表現される｡たいていの非述語的属性は､述語的属性に還元されたときに､日常言語の表現とは似ても似つかぬものになっている｡

例:「全ての人間のうち半分」､「すくなくとも果物の中のひとつ」､「典型的な赤さ」､「全ての属性をもつ」､「宇宙の全ての個別的事実」

例えば「全ての属性をもつ」は､「すべての属性をもつ」という属性をもつことになり､自己言及的なので非述語的属性に分類されている｡

「宇宙の全ての個別的事実」という個別的事実もその中に含まれていることになり､自己言及的なので非述語的属性である｡これらのケースは果物のクラスに果物というメンバーが含まれてはならない､というケースとはすこし違うという点に注意する必要がありそうだ｡

このように､「全ての属性」に言及していることが重要になっていきそうだ｡

・特に参考にしたページ
キーワード:非述語的属性
三浦俊彦『ラッセルのパラドックス』,81p

三浦俊彦『ラッセルのパラドックス』,84p

全体への量化を含む非可述的定義

非可述的属性は「全体への量化を含む非可述的定義」というように難しい言葉で表現されることがある｡「量化」とは一般に､論理式が適用される領域の個体の量を指定することらしい｡

量化だからといって全体へと言及しているとは限らないか､私にはよくわからない｡たとえば「１０個のうち､いくつかリンゴがある」という言い方は全体への量化を含んでいそうだが､「そのリンゴがひとつある」という命題は量化を含むが､全体への量化を含んでいなさそうである｡では､「そのひとつのxは典型的な赤いリンゴである」と表現しなおすとどうか､など様々な困惑はあるが､ひとまずそのように整理できそうだ｡

たとえば「量化詞」として「全ての」や「少なくとも１つの」､「ほとんどの」､「誰かが」､「誰もが」というような範囲を限定するような言葉がある｡これらの量化詞は､「全体への量化を含む」､つまり「全体に言及する量化詞」といえそうである｡

「典型的な」という言葉も「全体と多くの属性を共有している」と言い換えれば非可述的属性に近づいているとわかる｡言葉には隠れた､あるいは省略された要素があると考えると､複雑になっていくように感じる｡

「この世にある全ての人間のうち､すくなくとも一人は私だ」などという言葉ならわかりやすい｡

しかし､「すくなくともひとつは私の物だ」という場合はどうか｡通常は「そのひとつ以外の他のもの」があるという前提であり､それらの全体があるという前提で言及されていそうだ｡つまり､「そこにある全ての物のうち､すくなくともひとつは」というような全体への量化が含まれていそうだ｡

例えば「全てのリンゴ」を具体的に日常言語に置き換えるのは困難だろう｡「家にある全てのリンゴ」とより限定すればどうだろうか｡しかしリンゴが何を意味しているのか､あるいは家は何を意味しているのだろうか｡これでは曖昧である｡世界中の家かもしれないし､リンゴの絵も含まれるかもしれない｡「全てのリンゴ」はあのりんごと､そのリンゴと､近所のリンゴと､・・・と無限に足していった先の集合を表すような表現だろうか｡ものすごく限定すればたしかに可述的にはなりそうなイメージはあるが､いったいどのような限定をすれば適切なのだろうか｡

「少なくとも1つの属性」なども同様に難しそうだ｡オーダーを分けない場合は､「偉大な将軍に必要な属性」のうち､「少なくとも1つの属性」の中に「偉大な将軍に必要な属性」が入りかねない｡一つと言いながら､全ての属性をもっているという怪しい文章となる｡その場合は､第nオーダーの､と但し書きがあるとみればいいことを学んだ｡

たとえばベリーのパラドクスは「１９文字以内で名づけられない自然数の集合全体」への量化を含んでいるという｡このように考えていくと､「オーダーとは命題関数に含まれる量化を反映して設けられる階層のことである」という初見では意味不明な難しい表現もすこし理解することができる｡全体への量化を含んでそうな場合は高オーダー､含んでいなそうなら低オーダーと区別していくイメージである｡

・特に参考にしたページ
キーワード:全体への量化を含む非可述的定義

「ラッセルは、論理学の公理ではないこの原理を論理的に実装すべく、オーダーの理論を整備し、タイプ理論を意味論的パラドクスの生じないものとした。オーダーとは、命題関数に含まれる量化を反映して設けられる階層のことである。こうして作られた分岐タイプ理論では、オーダーnの命題関数への量化を含む命題関数のオーダーは、n+1になるとされる。よって、あるオーダーの命題関数全体に対する量化を含む命題関数は、それらよりも高いオーダーを持つ。先のベリーのパラドクスでは、自然数nのオーダーと名前(＊)のオーダーが区別され、意味論的パラドクスは解消される(Whitehead&Russell(1927)訳者「解説」および戸田山(2007)を参照)」
池田真治、伊藤遼、久木田水生「タイプ理論の起源と発展」53p

ナポレオンの例

「一九字以下で名づけられない最小の自然数」という例が私には数学的でイメージしにくい｡私の場合は三浦さんのナポレオンの例でより鮮明に理解することができた｡

たとえば「偉大な将軍に必要な全ての属性」は全体の量化を含んでいる｡なぜなら､「全て」という量化詞が使われているからである｡さらに､「偉大な将軍に必要な全ての属性」も属性であり､必要な属性であると考えると､自己言及的である｡

「偉大な将軍に必要なのは勇敢さだ」という文章では､「勇敢さ」に限定されているため､全体の量化を含んでいないのだろう｡とはいえ､例えば「勇敢さ」や「偉大な」､「必要な」､等々が「典型的な〇〇」の省略された形とみれば､非述語的属性をもってきそうだが､ここでは検討しないでおく｡しかしそうしたことを言い出すと「典型」ではない「完全な形」で言及することは難しいなと思ってしまう｡私はある単語に対して適当な､それこそ普通はこういう意味だろう､こういう要素を満たしていればOKだろうというような曖昧な使い方を普段しているからだ｡

「偉大な将軍に必要な全ての属性」というのがオーダーが高いというのは何となく理解できる｡

たとえば勇敢である､賢い､好色であるというような属性をあるタイプの中で最も低い属性=「可述的属性」だと仮定する｡

そうした列挙しうる属性を全て含んでいるような属性は､オーダーが高く､非可述的である｡たとえばみかんよりも果物のほうがタイプが高いと考える単純タイプ理論と類比的に考えると､すこしわかりやすい｡

たとえば三浦さんは「…性質を共有する」というような言い方は「非述語的属性」だという｡なぜなら､属性の全てに言及しているからだという｡「首都に必要な属性を少なくとも一つ持つ街に住む」なども非述語的属性を含んでいることになる｡「首都に必要な属性全て」に言及した言い方だからである｡

たとえば「偉大な将軍が必ずもつ属性のうち､少なくとも一つ持つ」という言い方をするとする｡これは「偉大な将軍が必ずもつ属性」という「全て」の属性にたしかに言及している｡そして具体的にどの属性かは言及されていない｡この高いオーダーだけの文章では､最も低いオーダーの属性がどれであるかは読み取ることができない｡つまり､可述的属性が特定されていない｡これも非可述的と表現できるのかもしれない｡

発言した本人の頭ではわかっているのかもしれないが､文章の中では読み取ることができず､可述的属性に還元することは難しい｡

AもしくはBもしくはCもしくはDもしくは・・と無限に続くような形なら可述的属性に還元することはできそうだが､日常言語で表現できそうにない､という意味で非可述的である｡そもそもそのように還元するためには本人が考えている集合全体が分かっているというような前提があるのではないかという疑問が生じるが､しかしここではあまり考えないでおくことにする｡このあたりはアプリオリに概念の本質がある､というような話と関連してくるのかもしれない(フッサールの本質直観へと接続する話)｡

以前､引用した図がこちら

・特に参考にしたページ
キーワード:ナポレオンの例
三浦俊彦『ラッセルのパラドックス』,78-79p

キーワード:「…性質を共有する」

三浦俊彦『ラッセルのパラドックス』,86-87p

機能等価としてワクワクする世界

われわれがいちいち具体的に還元して表現しないのは､困難であり､不便だからだろう｡曖昧に高オーダーを使ったほうが楽なのだ｡

実生活ではそれでもいいかもしれないが､しかし高オーダーばかり着目していて低オーダーの違いを軽視すると､学問上の問題が起きる｡社会学者のマートンが､マンハイムの概念が明確ではないと批判していたことと重なってくる｡仮説で最もらしいことを言っていたとしても､概念がルーズに使われている場合､仮説も結局はルーズになってしまうのであり､「分かった気になってしまう」のである｡

私が社会学や哲学を学んでいて思うことは､私が「分かった気になってしまう」という連続であるということだ｡「厳密に､それがどういう意味なのか具体的に､可述的属性に還元してください」と言われた場合､私はおそらく答えられないものが多いだろう｡曖昧に理解しているからである｡そもそも曖昧に説明されているからだ､という問題も一部あるかもしれないが､こういう視点が重要だという点は理解していくべきだろう｡

ベイトソン的な文脈で言えば両者を混同すると実生活において「病気」になるケースもある｡ユーモアにおいて意図的に混同するようなケースと違って､混同が当たり前となるような日常であり､本人は混同していると思っていないようなケースだろう｡たとえばアスペルガー症候群が相手の比喩を比喩だと受け取れないというケースを考えればわかりやすい(これは比喩だ､という言外のメッセージは論理階型(オーダー)がひとつ上のメタメッセージである)｡

ベイトソンの文脈で言えばこうした論理階型の混同は先天的な遺伝と後天的な環境の両方が関係しているという点がポイントなのだろう｡示唆的にポイントをとりあげるとすれば､「ある人物に論理階型を混同せざるをえなくさせた家庭環境とは？」という視点だろう｡

ここからが個人的に面白い｡社会学においてマートンやルーマンの「機能等価」で感じたようなワクワクがここにはある｡学問は面白いと感じる瞬間である｡ドアを開いて異なる世界に行って覗き見るような､そういう驚きがある｡それこそトランスコンテクスチュアルな状況であり､文脈を変えてある要素を解釈していくような連続である｡ドアをたくさん開くための大事なコード(鍵)だなと思う瞬間である｡

たとえば「美しい」とか「偉大である」というような普通の属性(可述的属性)すら､実は非可述的属性を省略形で述べたものである可能性が高いという｡

たとえば「この絵は美しい」と表現する時､「美しいというような理想型と多くの性質を共有する」という意味合いなのかもしれない｡

この高いオーダーでは具体的にどの属性をもっているのかがわからない｡「美しい絵が必ずもつ全ての属性」のうち､いったいどれだけ多くの具体的な属性をもっていれば我々は美しいと表現するのだろうか｡これは美学の動画で扱ったC.アレグザンダーの美学にもつながる視点である｡ちょうどアレグザンダーが「名付けえぬ質」と呼んでいたものが､「非可述的属性」とリンクして面白い｡」

私はモネのある絵がとても美しいと思うのだが､しかしあらゆる美しさの全てが当てはまるかというと､そうではないとも思ってしまう｡そもそもあらゆる美しさを私は言語化できない｡

「等価のものがあるという視点」は「還元公理」というものが関連してくるので､最後に取り上げることにする(後編の記事になります)｡

・特に参考にしたページ
キーワード:非述語的属性の省略形
「実際､『美しい』とか『偉大である』とか『健康である』のような普通の属性ですら､実は『理想型と多くの性質を共有する』のような非述語的属性を省略形で述べたものである可能性が高い｡述語的な属性に還元してから論じないと､頓珍漢な議論になったり､愚かな結論が導かれたりしかねない｡還元公理は､すべての哲学的議論で自覚されているべき仮定なのだ｡つまり､高オーダーの属性の存在を不要として見過ごすのではなく､その流通の現状をまず認めた上で､述語的属性への還元に備えねばならないということである｡右に見た『……性質を共有する』といった非述語的属性にちなんで､後期ウィトゲンシュタインの『家族的類似』を思い浮かべた人もいるだろう｡」
三浦俊彦『ラッセルのパラドックス』,87p

参考文献リスト

今回の主な文献

三浦俊彦「ラッセルのパラドクス: 世界を読み換える哲学 (岩波新書 新赤版 975)」

三浦俊彦「ラッセルのパラドクス: 世界を読み換える哲学 (岩波新書 新赤版 975)」

汎用文献

米盛裕二「アブダクション―仮説と発見の論理」

米盛裕二「アブダクション―仮説と発見の論理」

トーマス・クーン「科学革命の構造」

トーマス・クーン「科学革命の構造」

真木悠介「時間の比較社会学」

真木悠介「時間の比較社会学」

モリス・バーマン「デカルトからベイトソンへ ――世界の再魔術化」

モリス・バーマン「デカルトからベイトソンへ ――世界の再魔術化」

グレゴリー・ベイトソン「精神と自然: 生きた世界の認識論」

グレゴリー・ベイトソン「精神と自然: 生きた世界の認識論」

グレゴリー・ベイトソン「精神の生態学へ (上) (岩波文庫 青N604-2)」

グレゴリー・ベイトソン「精神の生態学へ (上) (岩波文庫 青N604-2)」

マックス・ウェーバー「社会科学と社会政策にかかわる認識の「客観性」」

マックス・ウェーバー「社会科学と社会政策にかかわる認識の「客観性」」

参考論文

・離散数学 | 植野真臣研究室 – 電気通信大学(URL)

・土屋盛茂「パラドックスとラッセルのタイプ理論」(URL)

・鈴木啓司「新たなる認識論理の構築14 : 集合論を超えて　境界についての認識論的考察」(URL)

・久木田水生「ラッセルの記述の理論とタイプ理論の関係について」(URL)

・池田真治、伊藤遼、久木田水生「タイプ理論の起源と発展」(URL)