創造法編集社

はじめに

要約

1. ピタゴラスは古代ギリシャの哲学者であり、数学者。
2. ピタゴラスは「万物は数である」と考えた。つまり、万物の根源(アルケー)は「数」であると考えた。
3. 数(アリスモス)とは数はそれ自体として比的なものであり、数と数の間の比的な関係をも意味している。自然数m：自然数n。(例)２：１など
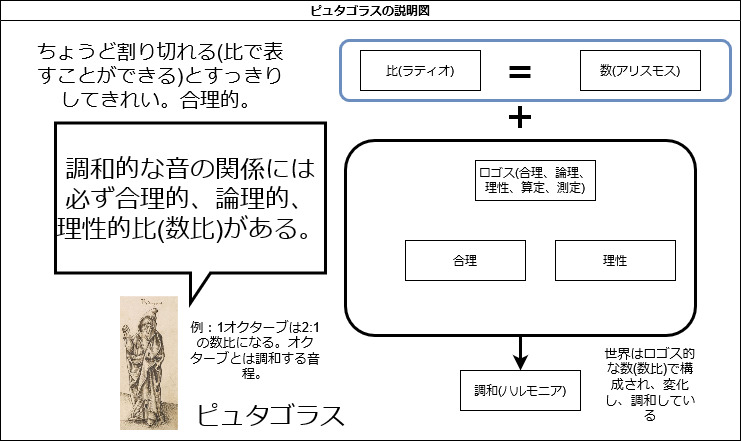
4. なぜピタゴラスは万物が数であると考えたのか。１：音楽における協和音２：天体の規則的な運行。調和的な音の関係は数比的な関係があると考え、実証した。音が数比によって調和するように、宇宙やその他すべての物事も数比によって調和すると考えた。数比こそ調和を生む原理。ピタゴラスはそうした数比が魂の浄化につながると考えた。

動画での解説・説明

・この記事のわかりやすい「概要・要約・要旨・まとめ」はyoutubeの動画の冒頭にありますのでぜひ参照してください｡

よろしければサイト維持のためにチャンネル登録をよろしくお願いしますm(_ _)mモチベになっていますm(_ _)m

ピタゴラス

ピタゴラスとは、意味

「ギリシャの哲学者、数学者。ピタゴラス教団という一種の宗教団体を結成し、南イタリアで貴族主義の党派の中心となる。数を万物の根本物質と考え、永遠の真理を教える手段として数学や音楽を重視。業績として、形象数、完全数、友愛数、数の比例の研究や、ピタゴラスの定理、無理数の発見、ピタゴラスの音階などが挙げられる。」

「ビジュアル図解シリーズ、哲学」、PHP、32-33P

「またピタゴラスについては，オルフェウス教との関係あるいはそれと関連して霊魂不滅説ないし輪廻説がしばしば取沙汰され，さらにはプラトン思想へのその影響が指摘されているが，それらはいずれも憶測の域を出ず，正確なところはわかっていないようである．これはピタゴラスが一冊の書物をも残さなかったということと関連があるであろう．」

小坂国継「初期ギリシア哲学者の実在感」,30P

ピタゴラス派とは、意味

・ピタゴラスは書物を残さなかったため、ピタゴラスが考えたのか、他のピタゴラス学派が考えたのか正確にわかってないことが多い。

→今回の記事では基本的にピタゴラスの考え≒ピタゴラス学派の考えとして扱っていく。

「この学派の中心人物であるピロラオス（Philolaos,前420頃）は「すべて認識されるものは数をもつ．数なくしては何一つ考えられることも認識されることもできない」（『断片集』第２部44章B4）といっている．」

小坂国継「初期ギリシア哲学者の実在感」,30P

アリスモス(数)

数と数比、調和の関係

アリスモス(数)とは、意味

例えば幸運は７である、という場合、単なる記号や単位以上の意味合いがある(ラッキーセブンの由来はピタゴラスのこうした考えにある)。ピタゴラスにおいて数と数比は同一のもと考えられている。

・数はそれ自体として比的なもの。ピタゴラスは数と数比、数学の原理、法則をあらゆるものの根源、原理だと考えた(万物の根源は数)。数こそ第一のものであり、数こそ存在の原理であり、生成の原理であると考えられている。つまり、万物は数から構成され、数によって変化すると考えられている。

「しかしピタゴラス学派にとって万物の本質である「数」（アリトモスἀριθμός）は，今日われわれが考えているような抽象的な記号や単位のようなものではなく，ある一定の大きさをもったものとして，つまりはそれ自身すぐれた意味での実在として考えられていた．」

小坂国継「初期ギリシア哲学者の実在感」,29P

数比とは、意味

→比例関係≒通約可能性があるということ≒分数で表せる≒スッキリする数

「数と数比とは基本的に同一のものとして捉えられる、という点にまず注意しておこう。数はそれ自体として比的なものである。」

杉村立男「ピタゴラス的合理主義の伝統」,86P

「数比とは整数m：整数nである。この段階では整数というより自然数というべきであるが、ある調和が成り立つということはこのような比的関係のうちにあるということであると理解されていた。それは例えば前述のようにハルモニアー、和音がまさにこのような比的関係であるということと同一のことがらである。すなわち数学的調和はそのまま音楽的調和であり、宇宙全体の調和である。ポルピュリオス「ピタゴラスは、諸天圏とそこを運動する諸星の全般的な調和〔音階〕を理解していたので、我々はその本性が貧弱なために聞くことが出来ないけれど、彼自身は全宇宙の調和（＝音楽、引用者）を聞いた。」8）（3～4世紀」

杉村立男「ピタゴラス的合理主義の伝統」,87P

「アリストテレスも『形而上学』において「『正方形の対角線はその辺と通約的である』ということは不可能であるといわれるが、…」4）、「およそ数は共通の単位で計られうるものすなわち通約的なものであり、…」5）といった用い方をしている。エウクレイデス『原論』でも「同じ尺度によって割り切られる量は通約できる量（シュムメトラメゲテー）といわれ、いかなる共通な尺度ももちえない量は通約できない量（アシュムメトラメゲテー）といわれる。」6）そしてピタゴラス的合理主義における比例とは本来この通約的な関係、すなわち比は常に整数m：整数nのかたちで表現できるはずのものであった」

杉村立男「ピタゴラス的合理主義の伝統」,86P

ハルモニアとは、意味

「比こそが世界の調和であるという点がその中心にある。アリストテレス「….彼ら（ピタゴラス派──引用者）はこの数学の原理をあらゆるものの原理であると考えた。数学の原理のうちでは、数が自然において第一のものであり、存在するものや生成するものとの多くの類似性は、火、土、水のうちによりも、むしろ数のうちに見られると考えたために、さらに音階についてもその特性や比例関係を数のうちに認めたので──要するに、数以外のものはその全本性において数に似ていると思われ、また数が自然全体のうちで第一のものであることから、数の基本要素を全てのあるものの基本要素であり、全宇宙は音階（ハルモニアー）であり、数であると考えたのである。そして、数や音階の中に宇宙の諸特性や諸部分、さらに宇宙の全秩序と一致しているのを示すことができるものがあれば、それらを集めて自分らの体系に適合させた。」1）（前4世紀）アエティオス「ピタゴラスは、哲学を最初にこの名前で呼んだ人であるが、数および数の間の比例関係──これを音階（ハルモニアー）と呼ぶ──を原理とし、これら二つのものから合成されたもの──これを幾何学的図形と呼ぶ──を基本要素としている。」2）（1あるいは2世紀）プロクロス「ピタゴラスが、幾何学の原理を上方より考察し、その定理を非物体的に、知性的に探究することによって、….彼こそが、比例についての教説と宇宙をかたちづくる─85─図形の構造とを発見したのである。」3）（5世紀）継承の筋道ははっきりしている。」

杉村立男「ピタゴラス的合理主義の伝統」,85-86P

ロゴスとは、意味

ピタゴラスにとって数の比がハルモニア(調和)を生むと考えられていた。ロゴスには合理的、理性的という意味があり、そして合理、理性という言葉はもともとラティオ(ratio)という「比」という意味合いがある。要するに、合理的、理性的、ロゴス的であることは数比的であり、そして調和的であることになる。

→英語で合理的、理性的を意味する言葉は「rational」。

「さて、「ロゴス」（……）という語のほうですが、これは「レゲイン」（……）という動詞に由来します。「レゲイン」には基本的に二つの意味があります。一つは「選ぶ」「より分ける」のそれであり、他は「数える」のそれであります。第一のものからは「言明」「文」「命題」「説明」「主張」「表現」等々の意味が出てき、第二のものからは「算定」とか「測定」とかの意味が出てくることになりました。「ロゴス」のこれら二つの基本的な意味のうち、重要なのは第一のもので、とりわけ「説明」としてのそれが、ギリシア哲学者の場合には最も重要なものとなっていきました。そして、「説明」としての「ロゴス」は、とりわけ、空想やイマジネーションを交えた「物語」風の「説明」としての「ミュトス」（神話）との対比においては、「合理的な討論にゆだねられ検討対象とされるものについて説明する言葉」という意味合いをもつこととなっていきましたが、この意味こそは、わたしたちの論題である「コスモロジー」という合成語に結晶しているものであると言うことができます。」

山川偉也「古代ギリシアのコスモロジー : 西洋思想史講義ノートより」,308-309P

理性とは、意味

合理的とは、意味

「合理的というのは、英語で言えばrational。この語はラテン語のratioから来ています。『理性』という意味ですが、本来の意味は『比』です。つまり、合理性という問題は、実は『数』、とりわけ『自然数』との関係があるのです。比とは、自然数の間の関係です。『２：１』とか『３：２』とか『４：３』とか。古代ギリシアには『ピタゴラスの定理』の名前の由来になっているピタゴラス教団という結社がありました。彼らは音楽を重視した。音楽の中にロゴスが働いている、と見たのです。そのように考えた理由は、まさに比ということに関係している。和音、つまり調和的な音の関係を見ると、そこには必ずきれいな比が利いているのです。たとえば、最も基本となる一オクターブ。それは弦の長さにして、ちょうど２：１の比になる音の関係です。他に五度とか四度というきれいな和音は、弦の長さの単純な比──３：２とか４：３とか──によって構成しうる。こうした事実の発見から、ピタゴラス教団は、音には合理性があり、そこに理性が作用していると考えた。合理性は、数の関係の中に美しく収まる感覚と深く結びついているのです。」

大澤真幸「社会学史」,320-321P

ピタゴラスの定理

例題１

辺Aが３、辺Bが２、斜線CがXの直角三角形におけるCの値を求めなさい。

ピタゴラスの定理により、3²+2²=C²になる。したがって、9+4=C²となり、13=C²になる。つまり、C=√13になる。

コラム：√ってなに・・・・？

平方根であるとは。「数に対して、平方すると元の値に等しくなる数のこと」になる。数 a に対して、x² = a を満たす x を a の平方根という。

また、√(ルート)は根号(こんごう)というらしい。英語ではradical symbolである。

たとえばx^2=4の場合、Xは2であり、2が平方根になる。それでは4を√で表現するとどうなるのか。√16である。√4^2ということになる。

例えば9なら、3に3を乗じれば9になる。しかし10は難しい。正の整数では計算できないらしい。このような平方根を無理数という。無理数とは有理数ではない実数である。

3.16227766017….と無限に続くらしい。このように無限に続く場合は無理数になるということだろうか。ちなみに3.1に3.1を乗じれば9.61になる。9.99999….と永遠に10にならないということだろうか。

3.16227766017..のようなスッキリしない数を便宜的に√10で表す、と考えると頭の悪い私でも理解できる。

同じように、√２もスッキリしない数で構成されている。1.41421356237….×1.41421356237….と永遠に続く。そのような数を√２と表せるのでスッキリする。

同じように、√13もスッキリしない数で構成されている。3.60555127546…×3.60555127546…と続く。

さて13=C^2がなぜC=√13になるのか。√13とは，二乗をすると13になるという数である。先程見たように、無理数である3.60555127546…に3.60555127546をかけると13にするというようにスッキリさせている。無限に続く数同士をかけられるのかなぜかわからないが、とりあえず無限にあるものはかけることも難しいので、無限と無限をかけたものであるという意味で√をつけたといったところだろうか。

さて、C＾２とは、Cの二乗という意味である。つまり、CにCをかけると、13になるという意味になる。それが13=C^2の意味である。

もし4=C^2なら、Cは２になる。なぜなら、2×2=4になるからである。

したがって、二乗をすると13になる数がCになる。しかし、先程見たように、正の整数では表現できない。3.60555127546となるからである。そこで、√という記号を使う。つまり√13になる。要するに、私の理解で言えばスッキリさせたいから√という記号を使うのである。これはスッキルートである。

有理数と無理数

有理数とは、意味

無理数とは、意味

無理数の存在を隠したかったピタゴラス。なぜ？

・ピタゴラスの考えでは世界は数、特に自然数(有理数、整数)の数比で構成されており、調和を保っている。しかし、自然数ではない数、すなわち非調和的、非合理的な数が存在することが判明してしまった。数の本質は比的なものという根本的な説が危うくなった。→世界には自然数で説明できない現象があることがわかったが、ピタゴラスはそれを隠そうとしたらしい。

・無理数を発見を公言したとされるピタゴラス学派のヒッパソスという人は、教団から追放され殺害されたという話もある。

・ピタゴラスの定理だけではなく、他にも黄金比における外中比でも同様に無理数が存在することがわかった。

「ピタゴラス教団が歴史的な実体としてどういうものだったのかよくわからないところもありますが、彼らは音楽と数に神秘的なつながりがあると考え、そこに合理性、世界の理性の働きを見ようとしたわけです。しかしなが、話はここで終わらない。『比で表すことができる』という合理性の原理から考えたときに、まさにその原理から始めたがゆえに、西洋の理性は、実は比で表しえないものが世界の中に必ずある、ということを発見してしまうのである。その発見をもたらしたのが、皮肉にもピタゴラス教団なのです。」

大澤真幸「社会学史」,322P

「X^２＝２・・・・・・①。ご存知のように、このｘは分数になりません。つまりXは、どのような自然数の比にもならないのです。合理性とは、自然数の比であるという見方を前提にすると、合理的な世界の把握のうちに収まらないものが存在している、ということになります。ですから、この比には回収できない数字ｘが存在しているということは、ピタゴラス教団にとっては、自分たちの基本的な教義を否定するスキャンダラスな事実でした。……さて、この問題は、自然数やその比によって定義できる数字(分数)とは異なる別種の数字、つまり『無理数』を導入することで解決されているわけです。①の方程式の解は、『√２』である、というぐあいにです。」

大澤真幸「社会学史」,323P

「世界のすべての現象や世界のすべての存在の本質原理が整数やその組み合せで説明できると考えるピタゴラス学派にとって，図形の性質を研究するうちに整数では説明できない事象に行き着いたのはなんとも皮肉な事態であった。「ピタゴラスの定理」によると長さが1の等辺直角三角形の斜辺の長さは冴という，まさしく無理数（不合理な数）となってしまうのである。ピタゴラス学派は√2(2乗して2となる数）が整数の比で表わせる数（有理数＝合理的な数）ではないことを実際に証明してしまった。秘密結社ピタゴラス学派はこの不測の事態に直面して，ピタゴラスの定理の正当性を疑う道を選ぶでもなく，整数が世界を支配しているという根本思想を覆す道を選ぶでもなく，斜辺が√2になってしまうというこの事実を封印して決して人見に触れないように隠し通す道を選ぶ。（ピタゴラス学派はこの事実を秘密結社外に漏そうとした者を処刑したとも伝えられている。）整数の原理や規則性が音楽の原理や規則性を完壁に説明できることを発見したピタゴラス学派にとって，世界のあらゆることも整数の規則性や原理で説明できるに違いないという確信は相当に強いものであった。それに矛盾する事実は封印しなければならない」

岡田,光弘「歪んだ真珠(バロック) : 音楽における規則性vs反規則性, またはロゴスvsパトス」,124P

万物存在論・生成論

万物は数であるとは、意味

ピタゴラス学派のピロラオスは「すべて認識されるものは数をもつ。数なくしては何一つ考えられることも認識されることもできない」と述べているらしい。

・なぜピタゴラスは「万物は数である」と考えたのか

1. 音楽における協和音(ピタゴラスの音律)
2. 天体の規則的な運行

１：音楽における協和音(ピタゴラスの音階)

音楽用語整理

・音程：ふたつの音の関係、隔たりのこと。異なった3個およびそれ以上の音が同時に響いたとき、これを和音(コード)という。

・オクターブ：西洋音楽における8度音程であり、周波数比2：1の音程。周波数が２対１の比率をもつ二つの音の音程関係。聴感上は同一音とさえ感じられ、同一音（完全1度音程）に次いでもっとも調和する音程。調和する音を「協和音」という。。

・周波数：「1 秒間の振動数」を意味する。振動数が細かい(多い、高い)ほど音が高くなる。ものすごく高い声を出せば薄いワイングラスが割れることもある(グラスは高い音と共振する)。

・音は「空気の振動」から生じるという。

・１弦の長さを半分にすれば、１オクターブ高い音ができる。

そしてそのできた２つの音はほとんど同じ音として聴こえ、同時に出すと「調和」する。イメージで言えば、低いドと高いドを同時に鳴らすような感じ。調和したドの音になる。

もちろん同じ高さの音を鳴らしても調和する(１度音程)。２：１の場合は８度音程という。

ドレミファソラシドというのは周波数がどんどん多くなり、音が高くなっていくイメージ。ドレミファソラシドで合計8度ある。つまり１オクターブ高い音ができ、一周する。ドから５度離れてる音はソ。ドとソを一緒に弾くと調和する(５度音程)。周波数の関係は３：２になる。

・調和する音の関係は８度音程だけか、というとそうではない。他にも５度音程、４度音程、１度音程という「完全協和音程」がある。８度音程は「２：１の比」５度音程は「３：２の比」、４度音程は「４：３の比」、１度音程は「１：１の比」となり、音が調和するらしい。

音の調和には数が関係している、それゆえに数は調和に関係し、数は万物の存在・生成に関与している

・音が調和する法則があり、その法則は「数とその比」が重要。→調和には数が関係していて、特に自然数(１，２，３….と数えられる正の整数)による数比が関係していると考えられた。

・この発想から、音だけではなく「すべてのもの」は数から構成され、数によって変化し、自然数(整数)の数比によって調和すると考えるに至った。つまり、「万物は数である」ということ。同時に、三平方の定理(ピタゴラスの定理)によって自然数ではない数字(無理数)が物事を構成する要素となることも分かってしまったが、ピタゴラスはそれを隠そうとした。

・ハンマーの話

・鍛冶屋の仕事場の前を通ったピタゴラスが、金床を打つハンマーの音が互いに協和しているのを聴き取った。彼がそれらのハンマーの重さを調べたところ、重さの比が2：1であれば調和することがわかった。

→数比が調和(ハルモニアー、協和音)に関係していることがわかった。数は音楽以外にも調和を生み出す根本的な要素なのではないか、という話につながっていく。宇宙も数比的調和に満たされていると考えていく。

「ハルモニア論の出発点はピタゴラスにある。古代ギリシアの時代において彼は、2つの音をつくりだす弦の長さの比、近代以降でいう振動数比が、数的に単純な比になっているほど協和して感じられること、複雑な比になっているほど不協和と感じられることを見出したとされている（伊藤氏報告論文p.62）。そしてこの発見にピタゴラスが至った経緯として、次のような言い伝えが今日でも知られている。鍛冶屋の仕事場の前を通ったピタゴラスが、金床を打つハンマーの音が互いに協和しているのを聴き取った。彼がそれらのハンマーの重さを調べたところ、重さの比が2：1であればオクターヴ（完全8度）、3：2であれば完全5度、4：3であれば、完全4度の協和音が生じることを解明した、というもの（1）である。このエピソードの真相はともかくとして、ピタゴラス派の人々は、ピタゴラスのハルモニア論を語り継ぎ、それを数学の一分野として発展させた。完全8度、完全5度、完全4度の3つの音程を、協和音（consonance）としたのである（2）。」

森薫「身体性の復権へ― 作曲の実践としてのハルモニア論を踏まえて ―」,110P

「ハルモニアーは我々から見ると絶妙な意味に用いられており、いわばこの点にこそピタゴラスの教説の要点がある。それは音階、和音、調和であるが、単に音楽の問題なのではない。すなわち、弦楽器において音階を定めていくのは、開放弦を単純な整数比m：nで分割していくと同時に、二本の弦を共に奏でたときに和音になるかどうかも、その二本の弦の長さの比が単純な整数比であるかどうかによって決まる。オクターヴ（8度）1：2，4度3：4，5度2：3。これもまたピタゴラス派の発見に帰せられる。そしてこのような数比的調和によって宇宙が満たされていると同時に、調和しているということはこのような数比的関係のうちにあるということとされるのである。」

杉村立男「ピタゴラス的合理主義の伝統」,86P

２：天体の規則的な運行

・ピタゴラスはイオニア学派から影響を受けている。たとえばアナクシマンドロスは宇宙を、地球を中心とした同心円構造だと考えた。ただし、地球は台形。

・ピタゴラスは地球をはじめて「球形」だと考えた。観察によるものではなく、球形は幾何学的に完全なものだという思考が先にあり、地球もそうであるはずという思考になってくる。また、地球は宇宙の中心にあると考えていた。

→「調和(ハルモニア)」が重要。円や球体は「調和の取れた図形」。天体の運動は調和が取れた状態を維持するために、等速円運動をしている”はず”だと考えた。

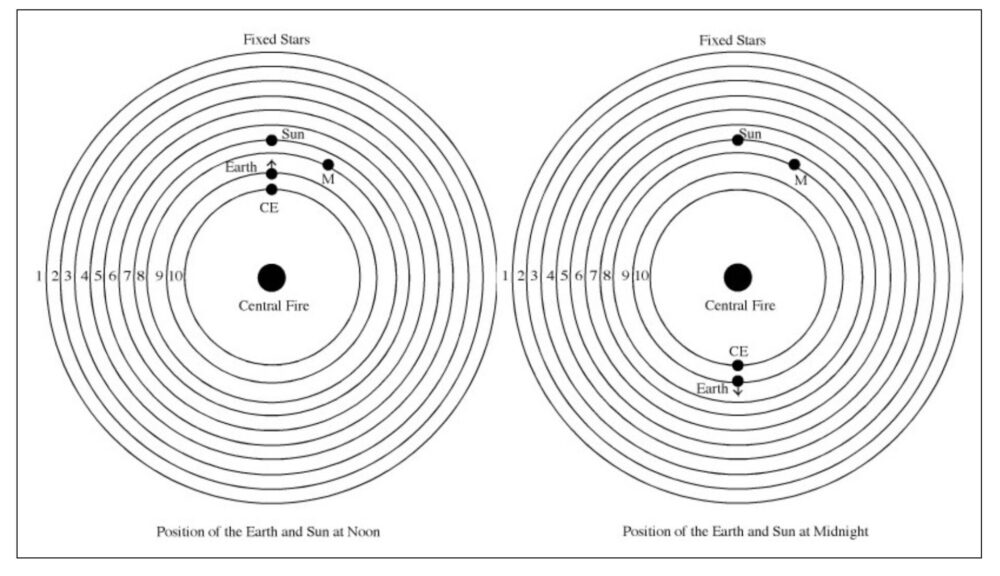
・ピタゴラス学派のピロラオスによる宇宙の図。宇宙の中心は地球ではなく、「中心火」があると考えられている。ピタゴラスの考えとは少しズレている。

・ピロラオスによれば、地球、日、月、火、水、木、金、土という肉眼で観測できる７つの天体がある。さらに地球、反地球、中心火の３つを足して合計１０の天体の数があると考えられている。

・１０という数は実測されたものではない(中心火や反地球というのは哲学的なもの)。ピタゴラス学派によれば「１０」という数は「完全な数」。

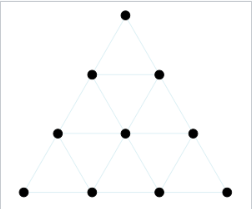
・１０＝１＋２＋３＋４で表現できるからだという。10個の点を三角形の形に配置した図をテトラクティスといい、ピタゴラス教団の紋章とされている。三角形が１０個の点で構成できるという数論、数の法則をまずは発見し、その法則は宇宙の天体にも同様にある”はず”だ、と類推していく。その大本が、数の法則によって音が調和するというエピソードにある。幾何学的に円は美しいので、地球も円、球体なはずだと類推していく。実際に観察したり科学的な根拠で球体だと分析したわけではない。

「この構想はいわゆる三法則も含まれる『世界の調和』（ハルモニケースムンディー1619年、＝『宇宙の和声学』）のうちにもそのまま持ち越されている。ケプラーにとっては、幾何学、天文学、音楽、人間精神等が全体として重なり合い、同一のものとして宇宙の調和的秩序をなしている。これはもちろん基本的枠組みにおいてピタゴラス的合理主義そのものであり、例えば「音楽と天文学の巧者たち（ピタゴラス派、引用者）が言うところによると、これらすべて〔全天〕は一種の調和を奏でつつすべてが同時に回転しているのだそうだからね」37）といったプラトンの著作を経て、伝えられた思想である」

杉村立男「ピタゴラス的合理主義の伝統」,97P

「ピタゴラス学派（BC6-5世紀) が考えた宇宙観は(1)地球は球形であり、(2)宇宙(コスモス）の 中心にあり、(3)その周りを惑星や恒星が同心円状に取り囲んでいるといったものでした。 「宇宙」という概念を最初に提唱し、幾何学的な思考を自然科学に適用し、 円や球といった「調和のとれた図形」が自然界を記述すると考えました。 また、天体の運動は「調和」がとれた状態を維持するために、等速円運動であると考えました。 この考え方は、これ以降の「地球中心説」の基本を構成することになりました。 ……この時期、様々な宇宙論が提出されました。フィロラオスの宇宙は、地球と、 日、月、火、水、木、金、土といった肉眼で観測できる天体、さらに ここへ中心火と反地球を足した10個の天体でこの宇宙は恒星されていると考えました。 中心火と反地球は哲学的なものであり、実測し確認したわけではありません。 太陽系の天体の数を”10=1+2+3+4”と表せるように人為的にこしらえたのです。」

出典

「ピロラオスによると、世界の中心には炎があり、最も高い場所ではさらなる炎が世界全体を囲っている。世界の本質として、まず中心が成り、その周りを10の神聖な天体が舞い回るー空、5つの惑星、太陽、月、地球、反地球があり、最後に世界の中心を占める暖炉の炎があると言う。周囲を覆う最も高い場所では、元素は純粋な状態にあり、彼はそこをオリンポスと呼んだ。オリンポス軌道より下の領域には、太陽と月をともなって5つの惑星があり、彼はそこを世界と呼んだ。さらにその下、月軌道の内側には地球を取り囲み変化と生成をもたらす場所があり、彼はそこを空と呼んだ。—ストバイオス, i. 22. 1d」

「フィロラオスまたはピロラオス（希: Φιλόλαος、Philolaos、紀元前470年頃 – 紀元前385年）は、ピタゴラス教団の一員、数学者であり、ソクラテス以前の哲学者である。万物は無限なるもの（無限定）と有限なるもの（限定）により生じるものをその基礎としており、両者は調和をもって結びついていると説いた。地球が宇宙の中心ではないという考えを述べた最初の人物であるとされる。」

出典

その他

宇宙をコスモスと呼んだ最初の人

「ピタゴラスは宇宙を，秩序と調和という意味をもつコスモス（κόσμος）と呼んだ最初の人である．この点についてアエティオス（Aetios１世紀頃）は「ピタゴラスは，万物を包み込むものを，そのなかにある秩序にもとづいてコスモスと名づけた最初の人であった」（『断片集』第２部第14章21）といっており……」

小坂国継「初期ギリシア哲学者の実在感」,30P

「アエティオス「ピタゴラスは、万有を包み込むものをその中にある秩序にもとづいてコスモス（秩序体）と名づけた最初の人であった。」14）もしそうだとすれば世界の秩序、すなわちよく配列されていること、が幾何学的なものであると考えられていたことは間違いない。」

杉村立男「ピタゴラス的合理主義の伝統」,90P

哲学という語をはじめて使った人

「しかし、ピタゴラスが最初に「哲学」と名付け、自身を哲学者と呼んだ。」（第一巻一二節）こうして哲学の系譜はギリシア人の中で辿られるが、その始まりはアナクシマンドロスとピタゴラスの二人におかれ、前者からイオニア派が、後者からイタリア派が発したとされる。」

納富信留「始まりを問う哲学史――複眼的ギリシア哲学史への試み」,53P

「ピタゴラスに哲学の始まりを帰す見方は、「哲学者φιλόσοφος」という語を彼が初めて語ったとの伝承による。他の候補が哲学という営みの始まりとされるのとは異なり、彼の場合は「哲学、哲学者」という概念の創始が主な理由となる。ディオゲネス・ラエルティオスはピタゴラスを「イタリア派」の系譜の祖に位置づけている。」

納富信留「始まりを問う哲学史――複眼的ギリシア哲学史への試み」,54P

霊魂不滅説(輪廻転生説、オルフェウス教との関連)

「またピタゴラスについては，オルフェウス教との関係あるいはそれと関連して霊魂不滅説ないし輪廻説がしばしば取沙汰され，さらにはプラトン思想へのその影響が指摘されているが，それらはいずれも憶測の域を出ず，正確なところはわかっていないようである．これはピタゴラスが一冊の書物をも残さなかったということと関連があるであろう．」

小坂国継「初期ギリシア哲学者の実在感」,30P

「けれどもよく考えてみるとオルフェウス教のいう『輪廻転生』は、この人生の終わったあとで霊魂が肉体を離れ、ひとまずハーデースの冥府に下って審判をうけ、生前の善業悪業に応じてふたたびべつの人間や動物の肉体のうちに宿るというものであるから、時間の円周性とはいちおう別のものである。このような因果応報のおしえと、出来事がある周期をもっていわば機械的に回帰するというピタゴラス学派の観念とのあいだには、時間意識のある確実な断層があるし……」

見田宗介「時間の比較社会学」,178-179P

「この学校は、研究機関というより一種の宗教団体で、その教義の特徴は、『魂は不滅で輪廻転生する』というものでした。ピタゴラスたちにとってもっとも重要なことは、不滅の魂の浄化であり、目には見えない数とその調和が世界を成り立たせていると考えることは、肉体からの魂の解放にもつながるものでした。」

「ビジュアル図解シリーズ、哲学」、PHP、32-33P

「ピタゴラス学派の根本思想は，万物の本質は数であるというもので，それゆえこの派の層々は皆紅学者であり，また天文学や音楽に通じていました。これら学問や技芸の根底にあるものは，やはり数の理念であるからです。また，ピタゴラスは前世の記憶を有していたと言われるところがら，入綾の魂は本来神々と共にある不死の存在なのだがこの世では肉体という濫に閉じ込められており，肉体の死と共にここから分離して冥府へ行き，ここで浄化され，再度他の肉体へ入るのであるという，ピタゴラス学派の霊魂観が生まれたもようです。プラトンの想起説は，ピタゴラス学派の輪廻転生説に多くを負っています。」

青山太郎「西洋文学における変身のテーマ」、3P

社会学との関連

貨幣と数の関係

１：貨幣とピタゴラスの関係

「世界のすべての事物をあたかも貨幣による価値づけのように数量としてとらえるということは、ピタゴラス学派においていっそう徹底される。」

(真木悠介『時間の比較社会学』,176P)

・ピタゴラス教団は貨幣(鋳貨)を鋳造していたという説がある

・イオニア地方は貨幣(鋳貨)の流通の発祥とされている地域。また、貨幣をはじめてつくったのは「イオニア地方のリュディアの王たち」とヘロドトスが伝えている。ピタゴラスが産まれたサモス島やタレス、アナクシマンドロスが活動したミレトスはイオニア地方にある。

・ピタゴラスはイタリアのギリシア植民地である商業都市クロトンに移住し、ピタゴラス教団を設立した。政治的支配権を獲得したとも言われている。

例：田中さんの労働力は１時間１０００円。田中さんの持っている宝石の価値は１０万円。りんごの価値は１００円、バナナの価値は１００円、みかんの価値も１００円。田中さんの宝石の価値はりんごの価値の1000倍です。これは客観的なものであり、客体化されたもの。しかし主観的には宝石よりりんごの方が価値があるかもしれません。質的なものや主観的なものではなく、量的で客観的なものが貨幣の性質にある。

・もし「質(固有性)」で換算されるなら、田中さんの労働力と佐藤さんの労働力は同じではない。しかし、(貨幣としての)「量(代替可能)」で換算されるなら、田中さんの労働力と佐藤さんの労働力は同じ１０００円となる。大切な人と過ごす1時間も、嫌いな人と過ごす1時間も、量的には同じ1時間となる。(客観的な)量や数で表現するシステムが貨幣。

・ピタゴラスも同様に、事物を「数」として表現しようとした。

→「万物は数である」という表現のように、すべてものごとが数で表現される。

理性は１、正義は４、好機は７、結婚は５、男性は偶数、女性は奇数、三角形の内角の和は180度、奇数の和は平方数になる・・・など。

→ピタゴラスが数にこだわった理由には、イオニア地方で貨幣がはじめて流通していたこととなにか関係があるのではないか、そういう文脈が基礎としてあるのではないか。

「世界のすべての事物をあたかも貨幣による価値づけのように数量としてとらえるということは、ピタゴラス学派においていっそう徹底される。ピタゴラスはアナクシメネスとほぼおなじころに、ミレトスの経済的なライヴァルであったおなじイオニアのサモスに生まれ、四十歳のころにイタリアの繁栄した商業都市クロトンに移住している。セルトマンによればピタゴラスはそこで、名高い彼の教団を創設するとともに、貨幣を鋳造しはじめた。この教団はやがて周辺のいくつかの繁栄した都市で政治的支配権を獲得する。そしてそれらの都市のいくつかにも、クロトンの鋳貨と同型の意匠をもった鋳貨があらわれはじめる。前六世紀の後半である。これらの鋳貨がピタゴラス教徒の造ったものであるということについては反論もあるが、慎重にみても、これらの地方で最初の鋳貨があらわれた時期と、ピタゴラス教団が広範な共鳴をえた時期とが重なるという事実は残る。鋳貨の特質は、とりわけその初期の素朴な鋳貨システムの特質は、事物を量として換算するのみではなく、それ以上分解しえない単位を基礎とする数として表現することである。<万有は数である>というピタゴラス学派の根本テーゼは、このような生活世界に基礎をおく宇宙了解であるように思われる。」

真木悠介「時間の比較社会学」,176-177P

時間意識と輪廻転生：円環としての時間

１：アナクシマンドロスやピタゴラスはオルフェウス教に影響を受けている

２：アナクシマンドロス＋ピタゴラス＝エムペドクレス

・ギリシャの「円環としての時間意識」が最初に生まれたのはアナクシマンドロスの哲学。「みずから発生してきたところの元のもとへ、もう一度帰ってゆくのが定めである」とアナクシマンドロスは述べた。アナクシマンドロスは万物の根源を「ト・アペイロン(無限定なもの、無限なもの)」と述べたのもポイント(なぜなら円環する時間も無限に循環するから)。

・ピタゴラス学派には「出来事がある周期のなかで回帰する」という時間の教えがある。

・エムペドクレスはミレトス学派とピタゴラス学派の両方から学び、「一つのものと多のものが時の円環のまわるにしたがって優勢を占める」と表現する。

→エムペドクレスにおいて円環する時間のイメージが完成する。

・ピタゴラス、アナクシマンドロスの時代は共動態(ゲマインシャフト)の解体期、集合態(ゲゼルシャフト)の発生期であり、貨幣がはじめて流通した時期だった。個人が共同態から自立し、疎外されていく。→貨幣の存在、社会のあり方が哲学(世界の認識)のあり方に影響を与えているのではないか。世界を客体的、数量的にみる認識は近代化においてより顕著となっていく。その近代化の起源のひとつにはヘレニズム文明があるのではないか(もういっぽうにはヘブライズムがある)。

・オルフェウス教における輪廻転生：人生が終わった後、霊魂から肉体が離れ、ハーデースの冥府に下って審判を受け、生前の善い行い、悪い行いに応じて別の人間や動物の肉体のうちに再び宿るという説。

→古代における「くりかえす逆転の反復、対極間を振動することの連続」、つまり「反復する時間」に近い。生死の反復する時間。

・ピタゴラスにおける輪廻転生：出来事がある周期をもっていわば機械的に回帰する。

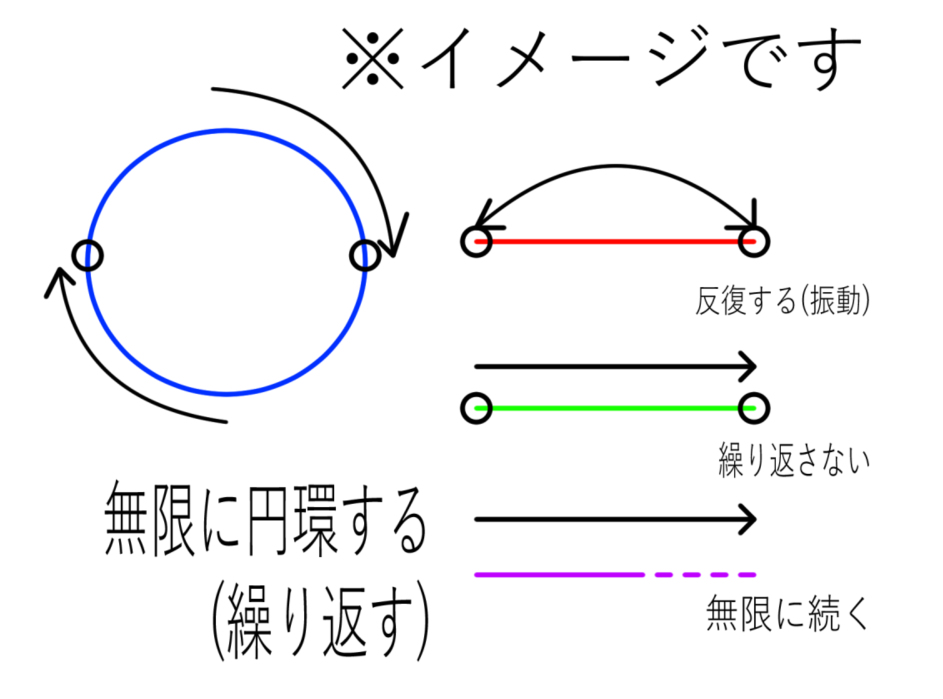
→オルフェウス教の時間と同じように「繰り返す」ものではあるが、反復というより循環的で円形的。ギリシャでは円形は「無限」を表すイメージでもあった。貨幣も同様に、「富には限りがない」とソロンがいったように、無限の性質をもっている。

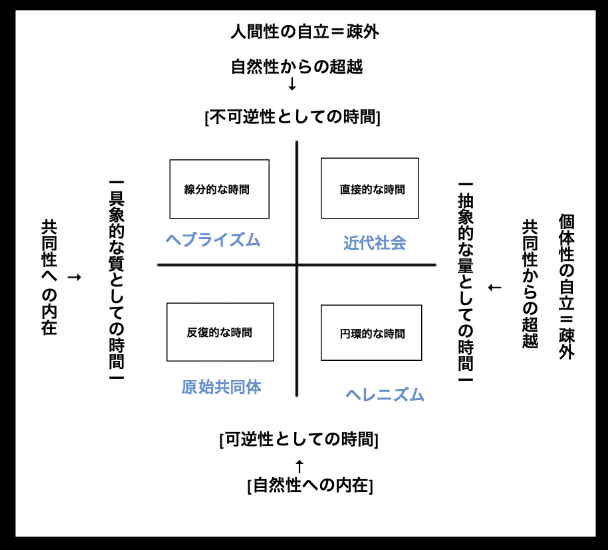
・オルフェウス教とピタゴラス教団の時間意識には違いがある。オルフェウス教の「具体的、非数量的な時間意識」と、ヘレニズム文明的な「数量的・抽象的・無限的な時間意識」が合わさり、ピタゴラス的な時間意識(円環としての時間意識)が生まれたのではないか。

→さらにこの「円環」という要素が「直線」としての時間に変わっていくと、数量的・不可逆的な時間意識、つまり近代的な時間意識に変わっていく。

図は真木悠介さんによるもの。

・オルフェウス教的な時間意識がヘレニズム文明以前の時間意識(反復的な時間)であると仮定するとわかりやすい。過去は潜在する現在。

・オルフェウス教の時間が貨幣や人口増大による共動態の解体などによって生まれたヘレニズム文明の時間意識と出会うことによって、「円環的な時間」が形成されていく。

・一方、ヘブライズム文明の時間意識はヘレニズム文明のように円環的・無限的ではなく、線分的な時間である。なぜなら、終末において神によって救済されるからである。それゆえに、時間は具体的で質的なものになる。

→近代の時間意識はヘレニズム＋ヘブライズムのようなもの。近代的な時間は抽象的・数量的かつ、不可逆的な時間。

「そして円関する時間のイメージをいっそう明確に把持したのは、『出来事がある周期のなかで回帰する』ことをおしえたピタゴラス学派のひとびとであり、アナクシマンドロスらのミレトス学派とピタゴラス学派双方の発想をうけたエムペドクレスのつぎのような表現において、円環する時間のイメージは完成される。『一つのものと多のものが時の円環のまわるにしたがって優勢を占める。』」

真木悠介「時間の比較社会学」,166-167P

「ピタゴラス学派についてはこのような汎数主義とならんで、オルフェウス教の影響がよく知られている。……このような因果応報のおしえと、出来事がある時期をもっていわば機械的に回帰するというピタゴラス学派の観念とのあいだには、時間意識のある確実な断層があるし、エムペドクレスの＜時の円環＞というふうにいっそう抽象化された時間のイメージは、オルフェウス教に還元しつくことはできない。オルフェウス教自体はむしろ、固有の意味でのヘレニズム文明以前の、農耕共同体の時間感覚を基礎としている。この時間感覚が、ヘレニズム文明の客体化し数量化する、したがってまた抽象的に無限化していくロゴスと出会った時に、その交叉するところに必然に生まれてくるのが、円環としての時間イメージであったのではないか。円形はギリシャの人間が無限を表象するときの形式であった。はるかな原始共同体にまで通底するオルフェウス教の生死の反復する感覚が、数量化するロゴスによって対象化されたときの形象が、ヘレニズム的な時間の円環であったはずである。」

真木悠介「時間の比較社会学」,178-197P

参考文献

参照論文(論文以外を含む)

1. 小坂国継「初期ギリシア哲学者の実在感」(URL)
2. 山川偉也「古代ギリシアのコスモロジー : 西洋思想史講義ノートより」(URL)
3. 杉村立男「ピタゴラス的合理主義の伝統」(URL)
4. 納富信留「始まりを問う哲学史――複眼的ギリシア哲学史への試み」(URL)
5. 森薫「身体性の復権へ― 作曲の実践としてのハルモニア論を踏まえて ―」(URL)
6. 青山太郎「西洋文学における変身のテーマ」(URL)
7. 岡田光弘「歪んだ真珠(バロック) : 音楽における規則性vs反規則性, またはロゴスvsパトス」(URL)

主要文献

「時間の比較社会学」

「時間の比較社会学」

汎用文献

「哲学 雑学3分間ビジュアル図解シリーズ」

「哲学 雑学3分間ビジュアル図解シリーズ」

「哲学用語図鑑」

「哲学用語図鑑」

「本当にわかる哲学」

「本当にわかる哲学」

「史上最強の哲学入門」

「史上最強の哲学入門」